题目内容
6.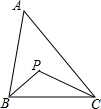 如图,在△ABC中,∠BAC=40°,点P是△ABC的内心,则∠BPC=( )
如图,在△ABC中,∠BAC=40°,点P是△ABC的内心,则∠BPC=( )| A. | 80 | B. | 110 | C. | 130 | D. | 140 |
分析 首先根据三角形内角和定理求得∠ABC+∠ACB,然后根据内心的定义证明∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB),然后根据三角形内角和定理求解.
解答 解:在△ABC中,∠ABC+∠ACB=180°-∠BAC=180°-40°=140°,
∵点P是△ABC的内心,
∴∠PBC=$\frac{1}{2}$∠ABC,∠PCB=$\frac{1}{2}$ACB,
∴∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×140=70°,
∴∠BPC=180°-(∠PBC+∠PCB)=180-70=110°.
故选B.
点评 此题主要考查了三角形的内心的计算,正确理解∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB)是关键.

练习册系列答案
相关题目
16.不等式组$\left\{\begin{array}{l}{x-1≤0}\\{6-3x>0}\end{array}\right.$的解集为( )
| A. | x≤1 | B. | x>-2 | C. | -2≤x≤1 | D. | 无解 |
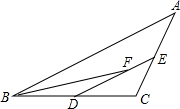 在△ABC中,D、E分别是BC、AC中点,BF平分∠ABC.交DE于点F.AB=8,BC=6,则EF的长为( )
在△ABC中,D、E分别是BC、AC中点,BF平分∠ABC.交DE于点F.AB=8,BC=6,则EF的长为( )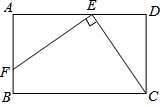 如图,在矩形ABCD中,EF⊥CE,EF=CE,DE=2cm,矩形的周长为32cm,求矩形ABCD的面积.
如图,在矩形ABCD中,EF⊥CE,EF=CE,DE=2cm,矩形的周长为32cm,求矩形ABCD的面积.
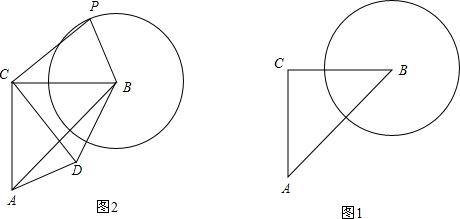
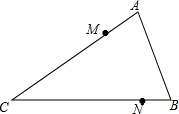 如图,在∠ACB内部求作一个点P,使PM=PN,且点P到CA、CB的距离相等.(尺规作图,不写作法,保留作图痕迹)
如图,在∠ACB内部求作一个点P,使PM=PN,且点P到CA、CB的距离相等.(尺规作图,不写作法,保留作图痕迹)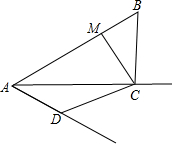 如图,AC平分∠BAD,CM⊥AB于M,且AB+AD=2AM,试求∠ADC+∠ABC的度数.
如图,AC平分∠BAD,CM⊥AB于M,且AB+AD=2AM,试求∠ADC+∠ABC的度数.