题目内容
16.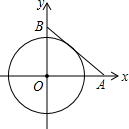 如图,长为10的线段AB的端点分别在x轴,y轴的正半轴上滑动(线段AB的长保持不变),⊙O与线段AB相切,则⊙O面积的最大值是( )
如图,长为10的线段AB的端点分别在x轴,y轴的正半轴上滑动(线段AB的长保持不变),⊙O与线段AB相切,则⊙O面积的最大值是( )| A. | 100π | B. | 25π | C. | 22π | D. | 20π |
分析 过O作OC⊥AB于C,设A(a,0),B(0,b),由⊙O与线段AB相切,确定OC=⊙O的半径r,根据a2+b2-2ab≥0,得到$ab≤\frac{{a}^{2}{+b}^{2}}{2}$,当ab=$\frac{{a}^{2}{+b}^{2}}{2}$时,r=$\frac{ab}{10}$最大,即r最大=$\frac{\frac{{a}^{2}{+b}^{2}}{2}}{10}$=5时,即可得到S最大=πr2=25π.
解答 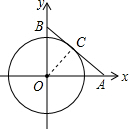 解:过O作OC⊥AB于C,
解:过O作OC⊥AB于C,
设A(a,0),B(0,b),
∵⊙O与线段AB相切,
∴OC=⊙O的半径r,
∵S△AOB=$\frac{1}{2}OA•OB=\frac{1}{2}AB•OC$,
∴r=$\frac{ab}{10}$,
∵a2+b2-2ab≥0,
∴$ab≤\frac{{a}^{2}{+b}^{2}}{2}$,
∴当ab=$\frac{{a}^{2}{+b}^{2}}{2}$时,
r=$\frac{ab}{10}$最大,
即r最大=$\frac{\frac{{a}^{2}{+b}^{2}}{2}}{10}$=5时,
S最大=πr2=25π,
故选B.
点评 本题考查了切线的性质,坐标与图形的性质,圆的面积,最大值问题,解答本题的关键是利用a2+b2-2ab≥0,这一重要不等关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.已知∠α的补角为125°12′,则它的余角为( )
| A. | 35°12′ | B. | 35°48′ | C. | 55°12′ | D. | 55°48′ |
4.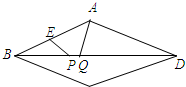 如图,已知菱形ABCD的边长为10,E为AB中点,对角线BD上有两个动点P,Q总保持PQ=2,若BD=16,则四边形AEPQ的周长最小值为( )
如图,已知菱形ABCD的边长为10,E为AB中点,对角线BD上有两个动点P,Q总保持PQ=2,若BD=16,则四边形AEPQ的周长最小值为( )
 如图,已知菱形ABCD的边长为10,E为AB中点,对角线BD上有两个动点P,Q总保持PQ=2,若BD=16,则四边形AEPQ的周长最小值为( )
如图,已知菱形ABCD的边长为10,E为AB中点,对角线BD上有两个动点P,Q总保持PQ=2,若BD=16,则四边形AEPQ的周长最小值为( )| A. | 16 | B. | 21 | C. | 7+$\sqrt{85}$ | D. | 7+$\sqrt{61}$ |
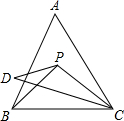 如图所示,P是等边△ABC内一点,PB=PC,∠PCD=∠PBA,且DC=BC,求∠D的度数.
如图所示,P是等边△ABC内一点,PB=PC,∠PCD=∠PBA,且DC=BC,求∠D的度数.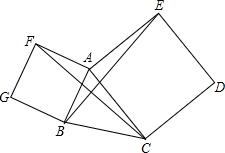 已知,如图,分别以△ABC的边AC,AB为边的三角形作正方形ACDE、BAFG.
已知,如图,分别以△ABC的边AC,AB为边的三角形作正方形ACDE、BAFG.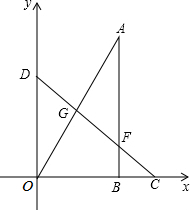 如图,将两块直角三角板摆放在平面直角坐标系中,有∠COD=∠ABO=Rt∠,∠OCD=45°,∠AOB=60°,且AO=CD=8.现将Rt△AOB绕点O逆时针旋转,旋转角为β(0°≤β≤180°).在旋转过程中,直线CD分别与直线AB,OA交于点F,G.
如图,将两块直角三角板摆放在平面直角坐标系中,有∠COD=∠ABO=Rt∠,∠OCD=45°,∠AOB=60°,且AO=CD=8.现将Rt△AOB绕点O逆时针旋转,旋转角为β(0°≤β≤180°).在旋转过程中,直线CD分别与直线AB,OA交于点F,G.