题目内容
20.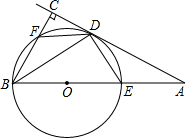 如图,BE是⊙O的直径,A是BE延长线上一点,过A点作⊙O的一条切线,切点为D,过B点作BC⊥AD于C,交⊙O于点F,连接BD.
如图,BE是⊙O的直径,A是BE延长线上一点,过A点作⊙O的一条切线,切点为D,过B点作BC⊥AD于C,交⊙O于点F,连接BD.(1)求证:DF=DE;
(2)若tanA=$\frac{1}{2}$,DC=3,求⊙O的半径.
分析 (1)连接OD,由AC是⊙O的切线,得到OD⊥AC,再由平行线的性质和等腰三角形的性质推出结论.
(2)由tanA=$\frac{1}{2}$,设⊙O的半径为r,则AD=2r,由勾股定理得;AO=$\sqrt{5}$r,根据平行线分线段成比例得到比例式C$\frac{AD}{CD}=\frac{AO}{OB}$,即可得到结果.
解答 解:(1)连接OD,
∵AC是⊙O的切线,
∴OD⊥AC,
∵BC⊥AD,
∴OD∥BC,
∴∠1=∠BDO,
∵OB=OD,
∴∠2=∠BDO,
∴∠1=∠2,
∴$\widehat{DF}$=$\widehat{DE}$,
∴DF=DE;
(2)∵tanA=$\frac{1}{2}$,
∴设⊙O的半径为r,则AD=2r,
由勾股定理得;AO=$\sqrt{5}$r,
∵OD∥BC,
∴C$\frac{AD}{CD}=\frac{AO}{OB}$,
∴$\frac{2r}{3}=\frac{\sqrt{5}r}{r}$,
∴r=$\frac{3\sqrt{5}}{2}$.
∴⊙O的半径为:$\frac{3\sqrt{5}}{2}$.
点评 本题考查了切线的性质,平行线的判定和性质,锐角三角函数,圆周角定理,连接OD是解题的关键.

练习册系列答案
相关题目
9.在下列函数中表示关于x的反比例函数的是( )
| A. | y=2x | B. | y=$\frac{2}{x}$ | C. | y=$\frac{2}{x+1}$ | D. | y=$\frac{2}{{x}^{2}}$ |
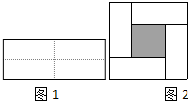 把一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后拼成一个正方形(如图1)
把一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后拼成一个正方形(如图1)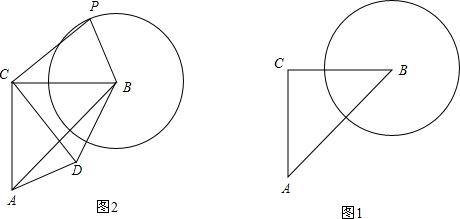
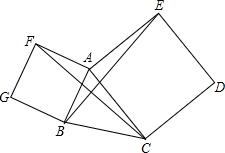 已知,如图,分别以△ABC的边AC,AB为边的三角形作正方形ACDE、BAFG.
已知,如图,分别以△ABC的边AC,AB为边的三角形作正方形ACDE、BAFG.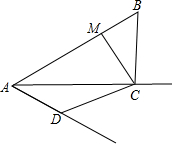 如图,AC平分∠BAD,CM⊥AB于M,且AB+AD=2AM,试求∠ADC+∠ABC的度数.
如图,AC平分∠BAD,CM⊥AB于M,且AB+AD=2AM,试求∠ADC+∠ABC的度数.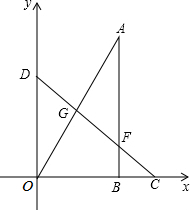 如图,将两块直角三角板摆放在平面直角坐标系中,有∠COD=∠ABO=Rt∠,∠OCD=45°,∠AOB=60°,且AO=CD=8.现将Rt△AOB绕点O逆时针旋转,旋转角为β(0°≤β≤180°).在旋转过程中,直线CD分别与直线AB,OA交于点F,G.
如图,将两块直角三角板摆放在平面直角坐标系中,有∠COD=∠ABO=Rt∠,∠OCD=45°,∠AOB=60°,且AO=CD=8.现将Rt△AOB绕点O逆时针旋转,旋转角为β(0°≤β≤180°).在旋转过程中,直线CD分别与直线AB,OA交于点F,G.