题目内容
18.已知反比例函数y=$\frac{k-1}{x}$的图象经过点(-2,1).(1)求k的值;
(2)判断下列各点否在这个图象上(-0.5,2),(4,-0.5),($\frac{1}{3}$,-6)
分析 (1)根据反比例好图象上点的坐标特征得到k-1=-2×1,然后解方程可得到k的值;
(2)利用(1)得到反比例函数解析式,然后根据反比例好图象上点的坐标特征分别判断三个点是否在反比例函数图象上.
解答 解:(1)把(-2,1)代入y=$\frac{k-1}{x}$得k-1=-2×1,
解得k=-1;
(2)反比例函数解析式为y=-$\frac{2}{x}$,
当x=-0.5时,y=4;x=4时,y=-0.5;当x=$\frac{1}{3}$,y=-6,
所以点(4,-0.5)和($\frac{1}{3}$,-6)在反比例函数图象上,而点(-0.5,2)不在反比例函数图象上.
点评 本题考查了反比例好图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,?ABED中,对角线BD平分∠ABE,过点D作DC∥AE,交BE的延长线于点C.求证:AB=CE.
如图,?ABED中,对角线BD平分∠ABE,过点D作DC∥AE,交BE的延长线于点C.求证:AB=CE.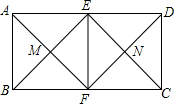 如图所示,在矩形ABCD中,AD=2AB,E,F分别是AD,BC的中点,连结AF与BE,CE与DF分别交于点M,N,连结EF,则图中一共有( )个正方形.
如图所示,在矩形ABCD中,AD=2AB,E,F分别是AD,BC的中点,连结AF与BE,CE与DF分别交于点M,N,连结EF,则图中一共有( )个正方形.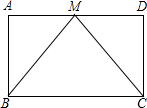 已知:如图,在?ABCD中,M是AD的中点,连接BM、CM,且BM=CM,求证:?ABCD是矩形.
已知:如图,在?ABCD中,M是AD的中点,连接BM、CM,且BM=CM,求证:?ABCD是矩形.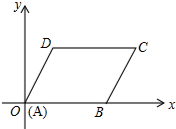 在平面直角坐标系中,?ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3).
在平面直角坐标系中,?ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3).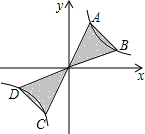 已知反比例函数y=$\frac{3}{x}$上有两点A,B,A点纵坐标是B点纵坐标的3倍,延长AO、BO交曲线的另一支于C,D两点,则图中阴影部分的面积为8.
已知反比例函数y=$\frac{3}{x}$上有两点A,B,A点纵坐标是B点纵坐标的3倍,延长AO、BO交曲线的另一支于C,D两点,则图中阴影部分的面积为8.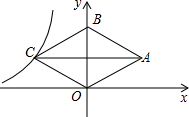 如图,在平面直角坐标系中,菱形OABC的顶点B在y轴正半轴上,菱形的两条对角线的长分别是6和4,函数y=$\frac{k}{x}(x<0)$的图象经过点C,则k的值为-6.
如图,在平面直角坐标系中,菱形OABC的顶点B在y轴正半轴上,菱形的两条对角线的长分别是6和4,函数y=$\frac{k}{x}(x<0)$的图象经过点C,则k的值为-6.