题目内容
3.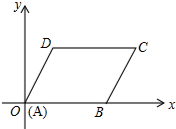 在平面直角坐标系中,?ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3).
在平面直角坐标系中,?ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3).(1)直接写出顶点C的坐标;
(2)求?ABCD的面积.
分析 (1)过点C作CE⊥OB于点E,由平行四边形的性质可知DC∥AB,所以点C的纵坐标和点D相同,再求出OE的长即可求出顶点C的坐标;
(2)由(1)可知OE,CE的长,所以由平行四边形的面积公式计算即可得到?ABCD的面积.
解答 解:
(1)过点C作CE⊥OB于点E,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∵D的坐标是(2,3).
∴点C的纵坐标为3,
∵顶点A,B的坐标是(0,0),(5,0),
∴OE=AB+BE=2+5=7,
∴点C的横坐标是7,
即点C的坐标是(7,3);
(2)∵点C的坐标是(7,3),
∴OE=7,CE=3,
∴?ABCD的面积=3×7=21.
点评 本题考查平行四边形的性质,平行四边形的对边相等,以及考查坐标与图形的性质等知识点.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
18.已知反比例函数y=$\frac{k-1}{x}$的图象经过点(-2,1).
(1)求k的值;
(2)判断下列各点否在这个图象上(-0.5,2),(4,-0.5),($\frac{1}{3}$,-6)
(1)求k的值;
(2)判断下列各点否在这个图象上(-0.5,2),(4,-0.5),($\frac{1}{3}$,-6)
8.若一个三角形三边长均为奇数,则此三角形( )
| A. | 一定是直角三角形 | B. | 一定是等腰三角形 | ||
| C. | 一定不是直角三角形 | D. | 一定不是等腰三角形 |
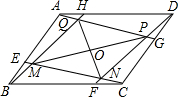 如图,在?ABCD中,AH=CF,BE=DG,连结AG,BH,CE,DF,交点分别为M,N,P,Q,若MP与NQ相交于O,求证:OM=OP,ON=OQ.
如图,在?ABCD中,AH=CF,BE=DG,连结AG,BH,CE,DF,交点分别为M,N,P,Q,若MP与NQ相交于O,求证:OM=OP,ON=OQ.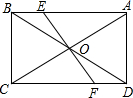 如图,已知在?ABCD中,对角线AC和BD相交于点O,EF过点O,且分别与AB,CD相交于点E、F,AB=10,BC=6,OF=3.2,求四边形AEFD的周长.
如图,已知在?ABCD中,对角线AC和BD相交于点O,EF过点O,且分别与AB,CD相交于点E、F,AB=10,BC=6,OF=3.2,求四边形AEFD的周长.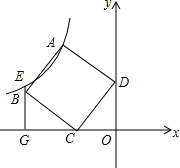 如图,在平面直角坐标系中,四边形ABCD为正方形,点C(-3,0),D(0,4),过B点作x轴的垂线交过A点的反比例函数图象于E点,交x轴于G点.
如图,在平面直角坐标系中,四边形ABCD为正方形,点C(-3,0),D(0,4),过B点作x轴的垂线交过A点的反比例函数图象于E点,交x轴于G点. 如图所示,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AD=3cm,求AB,AC的长.
如图所示,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AD=3cm,求AB,AC的长.