题目内容
10．点P1（x1，y1），P2（x2，y2）在反比例函数y=$\frac{k}{x}$（k＞0）的图象上，且x1=-x2，则y1=-y2．分析 根据反比例函数图象上点的坐标特征得k=x1•y1=x2•y2，然后把x1=-x2代入即可得到y1与y2的关系．
解答 解：根据题意得k=x1•y1=x2•y2，
而x1=-x2，
所以-x2•y1=x2•y2，
所以y1=-y2．
故答案为=-．
点评 本题考查了反比例函数图象上点的坐标特征：反比例函数y=$\frac{k}{x}$（k为常数，k≠0）的图象是双曲线，图象上的点（x，y）的横纵坐标的积是定值k，即xy=k．也考查了反比例函数的性质．
练习册系列答案
全优测试卷系列答案
冲刺100分1号卷系列答案
相关题目
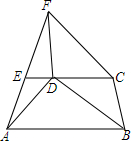如图．在?BCFD的对角线CD的延长线上取一点E，连接FE并延长至A点．使EA=EF，连接AB，求证：CE∥AB．
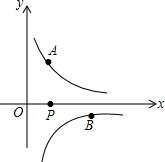如图，已知点A（$\frac{1}{2}$，y1），B（2，y2）分别为反比例函数y=$\frac{1}{x}$，y=$\frac{-1}{x}$图象上的点，动点P在x轴正半轴上运动，当线段AP与线段BP之差达到最大时，P的坐标是（$\frac{5}{2}$，0）．
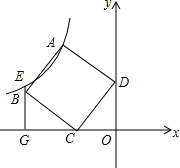如图，在平面直角坐标系中，四边形ABCD为正方形，点C（-3，0），D（0，4），过B点作x轴的垂线交过A点的反比例函数图象于E点，交x轴于G点．
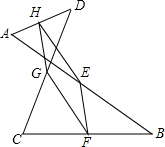如图，E、F、G、H分别是线段AB、CB、CD、AD的中点，连接E，F，G，H，判断四边形EFGH的形状，并说明理由．
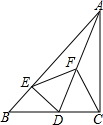如图，在Rt△ABC中，∠ACB=90°，D是边BC上一点，DE⊥AB于点E，点F是线段AD上一点，连接EF，CF．