题目内容
6.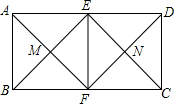 如图所示,在矩形ABCD中,AD=2AB,E,F分别是AD,BC的中点,连结AF与BE,CE与DF分别交于点M,N,连结EF,则图中一共有( )个正方形.
如图所示,在矩形ABCD中,AD=2AB,E,F分别是AD,BC的中点,连结AF与BE,CE与DF分别交于点M,N,连结EF,则图中一共有( )个正方形.| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 图中四边形ABFE、四边形EFCD、四边形EMFN是正方形,分别证明即可.
解答 解:∵四边形ABCD是矩形,AD=2AB,
∴AD=BC,AB=CD,∠ABC=∠BCD=∠BAD=∠ADC,AD∥BC,AB∥CD,
∴AE=ED=BF=FC=AB=CD,
∵AE=BF,AE∥BF,
∴四边形ABFE是平行四边形,
∵AB=AE,
∴四边形ABFE是菱形,
∵∠ABF=90°,
∴四边形ABFE是正方形,同理可以证明:四边形EFCD是正方形.
∴AF⊥BE,EC⊥DF,∠BEF=∠CEF=45°,EM=NF,
∴∠MEN=∠EMF=∠ENF=90°,
∴四边形EMFN是矩形,
∵EM=MF,
∴四边形EMFN是正方形.
故选D.
点评 本题考查矩形的性质、正方形的判定和性质等知识,灵活应用这些知识是解题的关键,记住正方形的三种判定方法,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.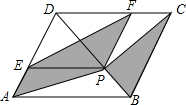 如图,菱形ABCD的边长为2,较短的对角线BD的长为$\sqrt{7}$,P是BD上一点,PE∥AB,PF∥AD,分别交菱形两边于点E、F,则图中阴影部分面积为( )
如图,菱形ABCD的边长为2,较短的对角线BD的长为$\sqrt{7}$,P是BD上一点,PE∥AB,PF∥AD,分别交菱形两边于点E、F,则图中阴影部分面积为( )
 如图,菱形ABCD的边长为2,较短的对角线BD的长为$\sqrt{7}$,P是BD上一点,PE∥AB,PF∥AD,分别交菱形两边于点E、F,则图中阴影部分面积为( )
如图,菱形ABCD的边长为2,较短的对角线BD的长为$\sqrt{7}$,P是BD上一点,PE∥AB,PF∥AD,分别交菱形两边于点E、F,则图中阴影部分面积为( )| A. | $\frac{3\sqrt{6}}{4}$ | B. | $\frac{3\sqrt{7}}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{3\sqrt{7}}{4}$ |
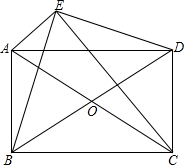 如图,点E为?ABCD外一点,AE⊥EC,BE⊥ED,对角线AC,BD交于点O.
如图,点E为?ABCD外一点,AE⊥EC,BE⊥ED,对角线AC,BD交于点O.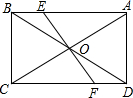 如图,已知在?ABCD中,对角线AC和BD相交于点O,EF过点O,且分别与AB,CD相交于点E、F,AB=10,BC=6,OF=3.2,求四边形AEFD的周长.
如图,已知在?ABCD中,对角线AC和BD相交于点O,EF过点O,且分别与AB,CD相交于点E、F,AB=10,BC=6,OF=3.2,求四边形AEFD的周长.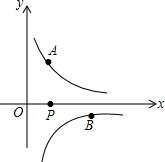 如图,已知点A($\frac{1}{2}$,y1),B(2,y2)分别为反比例函数y=$\frac{1}{x}$,y=$\frac{-1}{x}$图象上的点,动点P在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,P的坐标是($\frac{5}{2}$,0).
如图,已知点A($\frac{1}{2}$,y1),B(2,y2)分别为反比例函数y=$\frac{1}{x}$,y=$\frac{-1}{x}$图象上的点,动点P在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,P的坐标是($\frac{5}{2}$,0).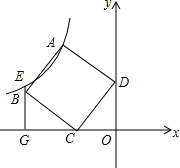 如图,在平面直角坐标系中,四边形ABCD为正方形,点C(-3,0),D(0,4),过B点作x轴的垂线交过A点的反比例函数图象于E点,交x轴于G点.
如图,在平面直角坐标系中,四边形ABCD为正方形,点C(-3,0),D(0,4),过B点作x轴的垂线交过A点的反比例函数图象于E点,交x轴于G点.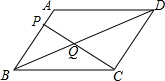 如图,在平行四边形ABCD中,点P在AB上,连接CP,交BD于点Q,当AP=$\frac{1}{4}$AB时,△BQC的面积为3,则平行四边形ABCD的面积为( )
如图,在平行四边形ABCD中,点P在AB上,连接CP,交BD于点Q,当AP=$\frac{1}{4}$AB时,△BQC的面积为3,则平行四边形ABCD的面积为( )