题目内容
9.化简:(1)$\frac{{a}^{2}-ab}{{a}^{2}}$÷$\frac{{a}^{2}{-b}^{2}}{{a}^{2}+2ab{+b}^{2}}$
(2)($\frac{1}{x-2}$-$\frac{2}{{x}^{2}-4x+4}$)×$\frac{x-2}{4-x}$.
分析 (1)原式利用除法法则变形,约分即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,约分即可得到结果.
解答 解:(1)原式=$\frac{a(a-b)}{{a}^{2}}$÷$\frac{(a+b)(a-b)}{(a+b)^{2}}$=$\frac{a(a-b)}{{a}^{2}}$•$\frac{(a+b)^{2}}{(a+b)(a-b)}$=$\frac{a+b}{a}$;
(2)原式=[$\frac{1}{x-2}$-$\frac{2}{(x-2)^{2}}$]•$\frac{x-2}{4-x}$=-$\frac{x-4}{(x-2)^{2}}$•$\frac{x-2}{x-4}$=-$\frac{1}{x-2}$=$\frac{1}{2-x}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
19.下列方程中不是二项方程的是( )
| A. | x2+x=0 | B. | $\frac{1}{3}{x}^{2}$+9=0 | C. | x5=1 | D. | 2-x4=3 |
14. 如图,已知AB=DC,下列所给的条件不能证明△ABC≌△DCB的是( )
如图,已知AB=DC,下列所给的条件不能证明△ABC≌△DCB的是( )
 如图,已知AB=DC,下列所给的条件不能证明△ABC≌△DCB的是( )
如图,已知AB=DC,下列所给的条件不能证明△ABC≌△DCB的是( )| A. | ∠A=∠D=90° | B. | ∠ABC=∠DCB | C. | ∠ACB=∠DBC | D. | AC=BD |
18.下列运算正确的是( )
| A. | m•m=2m | B. | (mn)3=mn3 | C. | (m2)3=m6 | D. | m6÷m2=m3 |
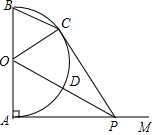 如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC,OC.
如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC,OC. 如图所示,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若△ABC的周长为10cm,则△OEC的周长为5cm.
如图所示,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若△ABC的周长为10cm,则△OEC的周长为5cm.