题目内容
10. 如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为弧BD的中点,若∠DAB=40°,则∠ABC=70°.
如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为弧BD的中点,若∠DAB=40°,则∠ABC=70°.
分析 连接AC,根据圆周角定理得到∠CAB=$\frac{1}{2}$∠DAB=20°,∠ACB=90°,计算即可.
解答 解: 连接AC,
连接AC,
∵点C为弧BD的中点,
∴∠CAB=$\frac{1}{2}$∠DAB=20°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ABC=70°,
故答案为:70°.
点评 本题考查的是圆周角定理的应用、圆内接四边形的性质,掌握半圆(或直径)所对的圆周角是直角是解题的关键.

练习册系列答案
相关题目
18.下列运算正确的是( )
| A. | m•m=2m | B. | (mn)3=mn3 | C. | (m2)3=m6 | D. | m6÷m2=m3 |
2.为了解居民用水情况,小明在某小区随机抽查了30户家庭的月用水量,结果如下表:
则这30户家庭的月用水量的众数和中位数分别是( )
| 月用水量/m3 | 4 | 5 | 6 | 8 | 9 | 10 |
| 户数 | 6 | 7 | 9 | 5 | 2 | 1 |
| A. | 6,6 | B. | 9,6 | C. | 9,6 | D. | 6,7 |
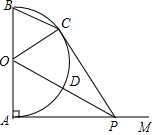 如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC,OC.
如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC,OC. 如图所示,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若△ABC的周长为10cm,则△OEC的周长为5cm.
如图所示,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若△ABC的周长为10cm,则△OEC的周长为5cm. 如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE. 如图,等边△ABC的边长为4,求高AD及△ABC的面积.
如图,等边△ABC的边长为4,求高AD及△ABC的面积.