题目内容
20.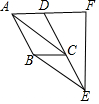 如图,四边形ABCD是平行四边形,E、F分别在DC、AD的延长线上,连接AC、BE,BE∥AC,EF⊥AD,垂足为F,AB=5,DF=4,则EF的长是( )
如图,四边形ABCD是平行四边形,E、F分别在DC、AD的延长线上,连接AC、BE,BE∥AC,EF⊥AD,垂足为F,AB=5,DF=4,则EF的长是( )| A. | $\sqrt{21}$ | B. | 2$\sqrt{21}$ | C. | 10 | D. | 8 |
分析 证明四边形ABEC是平行四边形,得出CE=AB=5,求出DE=CD+CE=10,再由勾股定理求出EF即可.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD=5,
∵BE∥AC,
∴四边形ABEC是平行四边形,
∴CE=AB=5,
∴DE=CD+CE=10,
∵EF⊥AD,
∴EF=$\sqrt{D{E}^{2}-D{F}^{2}}$=$\sqrt{1{0}^{2}-{4}^{2}}$=2$\sqrt{21}$;
故选:B.
点评 本题考查了平行四边形的性质与判定、勾股定理;熟练掌握平行四边形的判定与性质,由勾股定理求出EF是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.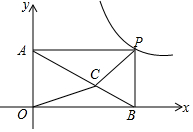 如图,P是双曲线y=$\frac{6}{x}$(x>0)上任意一点,作PB⊥x轴于B,PA⊥y轴于A,C是平行四边形OAPB内任意一点,连接CA、CO、CB、CP,则△OCB与△ACP的面积和等于( )
如图,P是双曲线y=$\frac{6}{x}$(x>0)上任意一点,作PB⊥x轴于B,PA⊥y轴于A,C是平行四边形OAPB内任意一点,连接CA、CO、CB、CP,则△OCB与△ACP的面积和等于( )
 如图,P是双曲线y=$\frac{6}{x}$(x>0)上任意一点,作PB⊥x轴于B,PA⊥y轴于A,C是平行四边形OAPB内任意一点,连接CA、CO、CB、CP,则△OCB与△ACP的面积和等于( )
如图,P是双曲线y=$\frac{6}{x}$(x>0)上任意一点,作PB⊥x轴于B,PA⊥y轴于A,C是平行四边形OAPB内任意一点,连接CA、CO、CB、CP,则△OCB与△ACP的面积和等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
12.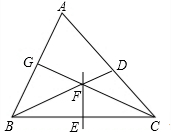 如图,△ABC中,BD是∠ABC的平分线,EF垂直平分BC分别交BC,BD与点E,F,连接CF并延长,交AB于点G,若CG⊥AB,则∠FCB的度数为( )
如图,△ABC中,BD是∠ABC的平分线,EF垂直平分BC分别交BC,BD与点E,F,连接CF并延长,交AB于点G,若CG⊥AB,则∠FCB的度数为( )
 如图,△ABC中,BD是∠ABC的平分线,EF垂直平分BC分别交BC,BD与点E,F,连接CF并延长,交AB于点G,若CG⊥AB,则∠FCB的度数为( )
如图,△ABC中,BD是∠ABC的平分线,EF垂直平分BC分别交BC,BD与点E,F,连接CF并延长,交AB于点G,若CG⊥AB,则∠FCB的度数为( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
9. 如图,在Rt△ABC中,∠C=90°,如果AB=5,BC=3,那么AC等于( )
如图,在Rt△ABC中,∠C=90°,如果AB=5,BC=3,那么AC等于( )
 如图,在Rt△ABC中,∠C=90°,如果AB=5,BC=3,那么AC等于( )
如图,在Rt△ABC中,∠C=90°,如果AB=5,BC=3,那么AC等于( )| A. | $\sqrt{34}$ | B. | 3 | C. | 4 | D. | 5 |
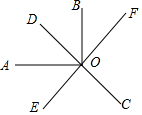 如图,已知直线CD、EF相交于点O,OA⊥OB,且OE平分∠AOC,若∠EOC=60°,则∠BOF=30°.
如图,已知直线CD、EF相交于点O,OA⊥OB,且OE平分∠AOC,若∠EOC=60°,则∠BOF=30°. 如图,在△ABC中,∠ABC=90°,AB=12,BC=5,若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
如图,在△ABC中,∠ABC=90°,AB=12,BC=5,若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )