题目内容
12．
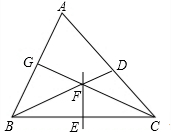如图，△ABC中，BD是∠ABC的平分线，EF垂直平分BC分别交BC，BD与点E，F，连接CF并延长，交AB于点G，若CG⊥AB，则∠FCB的度数为（ ）| A． | 30° | B． | 35° | C． | 40° | D． | 45° |
分析 根据线段垂直平分线的性质得到FB=FC，得到∠FBC=∠FCB，根据角平分线的定义得到∠FBC=∠GBF，根据三角形内角和定理计算即可．
解答 解：∵EF是BC的垂直平分线，
∴FB=FC，
∴∠FBC=∠FCB，
∵BD是∠ABC的平分线，
∴∠FBC=∠GBF，
∵CG⊥AB，
∴∠BGC=90°，
∴∠FCB=30°，
故选：A．
点评 本题考查的是线段垂直平分线的性质、角平分线的定义以及三角形内角和定理，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．
练习册系列答案
相关题目
2．下列各式中，是分式的是（ ）
| A． | $\frac{x}{2}$ | B． | $\frac{1}{3}$x2 | C． | $\frac{x}{π}$ | D． | $\frac{2x+1}{x-3}$ |
20．
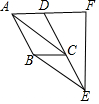如图，四边形ABCD是平行四边形，E、F分别在DC、AD的延长线上，连接AC、BE，BE∥AC，EF⊥AD，垂足为F，AB=5，DF=4，则EF的长是（ ）
如图，四边形ABCD是平行四边形，E、F分别在DC、AD的延长线上，连接AC、BE，BE∥AC，EF⊥AD，垂足为F，AB=5，DF=4，则EF的长是（ ）| A． | $\sqrt{21}$ | B． | 2$\sqrt{21}$ | C． | 10 | D． | 8 |
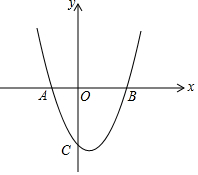如图，在平面直角坐标系中，已知抛物线y=$\frac{3}{2}$x2+bx+c与x轴交于A（-1，0），B（2，0）两点，与y轴交于点C．
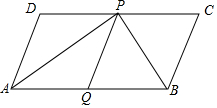如图，在?ABCD中，AP和BP分别平分∠DAB和∠CBA，PQ∥AD，若AD=5cm，AP=8cm，则△ABP的面积等于24cm2．
如图，∠A=2∠ABC，BD平分∠ABC，且AD∥BC，请运用所学知识，求∠ADB的度数．
2．下列依次给出的点的坐标（0，3），（1，1），（2，-1），（3，-3），…，依此规律，则第2017个点的坐标为（ ）
| A． | （2017，-2015） | B． | （2016，-2014） | C． | （2016，-4029） | D． | （2016，-4031） |