Question

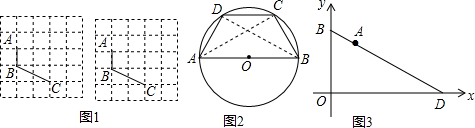
5．如图，以Rt△ABC直角边BC为直径作⊙O，交AB边于点D，已知AC=2，∠B=30°，则阴影部分面积为$\frac{5\sqrt{3}}{4}$-$\frac{π}{2}$．

Answer 1

分析 由∠A的度数求出∠ADO度数，利用30°直角三角形的性质求出BC的长，利用勾股定理求出AC的长，阴影部分面积=直角三角形ABC面积-扇形OCD面积-三角形AOD面积，求出即可．

解答 解：连接半圆圆心O与D，过点O作OE⊥AB，
在Rt△ABC中，∠B=30°，AC=2，
∴∠COD=60°，BC=2$\sqrt{3}$
∴OB=$\sqrt{3}$，
∴OE=$\frac{\sqrt{3}}{2}$，BE=$\frac{3}{2}$，
∴BD=3，
则S_阴影=S_△ABC-S_扇形COD-S_△BOD=$\frac{1}{2}$×2×2$\sqrt{3}$-$\frac{60•π•（\sqrt{3}）^{2}}{360}$-$\frac{1}{2}$×3×$\frac{\sqrt{3}}{2}$=$\frac{5\sqrt{3}}{4}$-$\frac{π}{2}$，
故答案为：$\frac{5\sqrt{3}}{4}$-$\frac{π}{2}$．

点评 本题考查了扇形面积的计算，涉及的知识有：等腰三角形的性质，含30°直角三角形的性质，以及勾股定理，熟练掌握扇形面积公式S=$\frac{nπ{r}^{2}}{360}$是解本题的关键．