题目内容
12.已知a2(b+c)=b2(a+c)=2015,且a,b,c互不相等,则c2(a+b)-2014的值为( )| A. | 0 | B. | 1 | C. | 2015 | D. | -2015 |
分析 由a2(b+c)=b2(a+c)=2015得a2(b+c)-b2(a+c)=0,左边因式分解可得(a-b)(ab+ac+bc)=0,从而有ab+ac+bc=0,结合b2(a+c)=2015知-abc=2015,将原式变形可得c2(a+b)-2014=-abc-2014,代入即可得答案.
解答 解:∵a2(b+c)=b2(a+c)=2015,
∴a2(b+c)-b2(a+c)=0,
a2b+a2c-ab2-b2c=0,
ab(a-b)+c(a+b)(a-b)=0,
(a-b)(ab+ac+bc)=0,
∵a,b,c互不相等,即a-b≠0,
∴ab+ac+bc=0,
又∵b2(a+c)=2015,即b(ab+bc)=2015,
∴b•(-ac)=2015,即-abc=2015,
则c2(a+b)-2014=c(ac+bc)-2014
=c•(-ab)-2014
=-abc-2014
=2015-2014
=1.
故选:B.
点评 本题主要考查因式分解的应用,由a2(b+c)-b2(a+c)=0因式分解得(a-b)(ab+ac+bc)=0,从而得到-abc=2015是解决此题的关键,将已知条件经过变形使其与待求代数式联系到一起是解题的思路.

练习册系列答案
相关题目
2.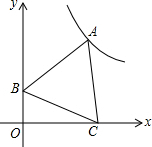 如图,点A是反比例函数y=$\frac{12\sqrt{3}}{x}$(x>0)图象上一点,点C是x正半轴上一点,点B的坐标为(0,$\sqrt{3}$),当△ABC是等边三角形时,点A的坐标为( )
如图,点A是反比例函数y=$\frac{12\sqrt{3}}{x}$(x>0)图象上一点,点C是x正半轴上一点,点B的坐标为(0,$\sqrt{3}$),当△ABC是等边三角形时,点A的坐标为( )
 如图,点A是反比例函数y=$\frac{12\sqrt{3}}{x}$(x>0)图象上一点,点C是x正半轴上一点,点B的坐标为(0,$\sqrt{3}$),当△ABC是等边三角形时,点A的坐标为( )
如图,点A是反比例函数y=$\frac{12\sqrt{3}}{x}$(x>0)图象上一点,点C是x正半轴上一点,点B的坐标为(0,$\sqrt{3}$),当△ABC是等边三角形时,点A的坐标为( )| A. | (3$\sqrt{3}$,4) | B. | (4,3$\sqrt{3}$) | C. | (4$\sqrt{3}$,3) | D. | (3,4$\sqrt{3}$) |
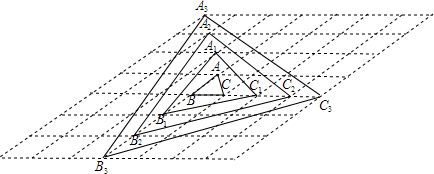
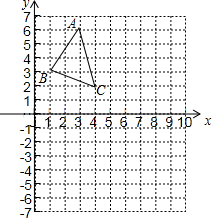 如图,△ABC的顶点坐标分别是A(3,6)、B(1,3)、C(4,2).
如图,△ABC的顶点坐标分别是A(3,6)、B(1,3)、C(4,2).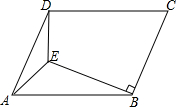 如图,E是?ABCD内一点,ED⊥CD,EB⊥BC,∠AED=135°,连CE交AD于F.
如图,E是?ABCD内一点,ED⊥CD,EB⊥BC,∠AED=135°,连CE交AD于F.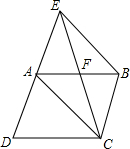 如图,已知E为?ABCD的边DA的延长线上的一点,且AE=AD,EC交AB于点F,那么,EF=CF吗?为什么?
如图,已知E为?ABCD的边DA的延长线上的一点,且AE=AD,EC交AB于点F,那么,EF=CF吗?为什么?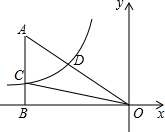 如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-8,6),则△AOC的面积为18.
如图,已知双曲线y=$\frac{k}{x}$(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-8,6),则△AOC的面积为18.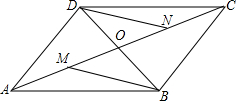 如图所示,?ABCD的对角线AC,BD相交于O,M是AO的中点,N是CO的中点,则BM与DN有什么关系?证明你的结论.
如图所示,?ABCD的对角线AC,BD相交于O,M是AO的中点,N是CO的中点,则BM与DN有什么关系?证明你的结论.