题目内容
20.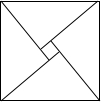 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示.如果大正方形的面积是l3,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2值为( )
2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示.如果大正方形的面积是l3,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2值为( )| A. | 25 | B. | 9 | C. | 13 | D. | 169 |
分析 根据大正方形的面积即可求得c2,利用勾股定理可以得到a2+b2=c2,然后求得直角三角形的面积即可求得ab的值,根据(a+b)2=a2+b2+2ab=c2+2ab即可求解.
解答  解:如图,∵大正方形的面积是13,
解:如图,∵大正方形的面积是13,
∴c2=13,
∴a2+b2=c2=13,
∵直角三角形的面积是(13-1)÷4=3,
又∵直角三角形的面积是$\frac{1}{2}$ab=3,
∴ab=6,
∴(a+b)2=a2+b2+2ab=c2+2ab=13+2×6=13+12=25.
故选:A.
点评 本题考查了勾股定理以及完全平方公式.注意完全平方公式的展开:(a+b)2=a2+b2+2ab,还要注意图形的面积和a,b之间的关系.

练习册系列答案
相关题目
10. 如图,把一块三角板的直角顶点放在直尺的一边上,如果∠1=30°,那么∠2为( )
如图,把一块三角板的直角顶点放在直尺的一边上,如果∠1=30°,那么∠2为( )
 如图,把一块三角板的直角顶点放在直尺的一边上,如果∠1=30°,那么∠2为( )
如图,把一块三角板的直角顶点放在直尺的一边上,如果∠1=30°,那么∠2为( )| A. | 60° | B. | 30° | C. | 70° | D. | 50° |
11. 如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD,BD,则下列结论:
如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD,BD,则下列结论:
①AD=BC=CE;
②BD,AC互相平分;
③四边形ACED是菱形;
④四边形ABED的面积为$\frac{3\sqrt{3}}{4}$AB2.
其中正确的个数是( )
 如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD,BD,则下列结论:
如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD,BD,则下列结论:①AD=BC=CE;
②BD,AC互相平分;
③四边形ACED是菱形;
④四边形ABED的面积为$\frac{3\sqrt{3}}{4}$AB2.
其中正确的个数是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
8.下列运算中错误的是( )
| A. | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{6}$ | B. | $\sqrt{8}$÷$\sqrt{2}$=2 | C. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | D. | (-$\sqrt{3}$)2=3 |
5. 小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:
小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)频数分布直方图的组距是多少?这个组距选择得好不好?请判断并说明理由.
(3)如果家庭人均月收入“大于999不足1600元”的为中等收入家庭,请你通过样本估计总体中的中等收入家庭大约有多少户?
 小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:
小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:| 分组 | 频数 | 频率 |
| 600~799 | 2 | 0.050 |
| 800~999 | 6 | 0.150 |
| 1000~1199 | 0.450 | |
| 1200~1399 | 9 | 0.225 |
| 1400~1599 | ||
| 1600~1799 | 2 | 0.050 |
| 合计 | 40 | 1.000 |
(2)频数分布直方图的组距是多少?这个组距选择得好不好?请判断并说明理由.
(3)如果家庭人均月收入“大于999不足1600元”的为中等收入家庭,请你通过样本估计总体中的中等收入家庭大约有多少户?
9.下列长度的各组线段能组成一个三角形的是( )
| A. | 3cm,5cm,8cm | B. | 1cm,2cm,3cm | C. | 4cm,5cm,10cm | D. | 3cm,4cm,5cm |
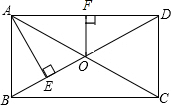 如图,在矩形ABCD中,对角线AC、BD交于点O,自点A作AE⊥BD于点E,且BE:ED=1:3,过点O作OF⊥AD于点F,若OF=3cm,则BD的长为( )cm.
如图,在矩形ABCD中,对角线AC、BD交于点O,自点A作AE⊥BD于点E,且BE:ED=1:3,过点O作OF⊥AD于点F,若OF=3cm,则BD的长为( )cm. 如图,某滑板爱好者训练时的斜坡示意图,出于安全因素考虑,决定将训练的斜坡的倾角由45°降为30°,已知原斜坡坡面AB的长为5米,点D、B、C 在同一水平地面上.
如图,某滑板爱好者训练时的斜坡示意图,出于安全因素考虑,决定将训练的斜坡的倾角由45°降为30°,已知原斜坡坡面AB的长为5米,点D、B、C 在同一水平地面上.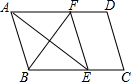 如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )
如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )