题目内容
15.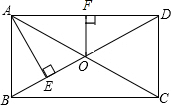 如图,在矩形ABCD中,对角线AC、BD交于点O,自点A作AE⊥BD于点E,且BE:ED=1:3,过点O作OF⊥AD于点F,若OF=3cm,则BD的长为( )cm.
如图,在矩形ABCD中,对角线AC、BD交于点O,自点A作AE⊥BD于点E,且BE:ED=1:3,过点O作OF⊥AD于点F,若OF=3cm,则BD的长为( )cm.| A. | 6 | B. | 9 | C. | 12 | D. | 15 |
分析 根据矩形的性质得出AC=BD,BD=2BO=2OD,AC=2AO,∠BAD=90°,求出AO=BO,根据等边三角形的判定得出△ABO是等边三角形,求出∠BAO=60°,∠DAO=30°,即可求出AO,即可求出答案.
解答 解:∵四边形ABCD是矩形,
∴AC=BD,BD=2BO=2OD,AC=2AO,∠BAD=90°,
∴AO=BO,
∵BE:ED=1:3,
∴BE=EO,
∵AE⊥BD,
∴AB=AO,
即AO=OB=AB,
∴△ABO是等边三角形,
∴∠BAO=60°,
∴∠DAO=90°-60°=30°,
∵OF⊥AD于点F,OF=3cm,
∴∠AFO=90°,AO=2OF=6cm,
∴AC=2AO=12cm,
∴BD=12cm,
故选C.
点评 本题考查了等边三角形的性质和判定,含30°角的直角三角形性质,矩形的性质的应用,能熟记知识点的内容是解此题的关键,注意:矩形的对角线互相平分且相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.在下列事件调查中,适宜采用全面调查的是( )
| A. | 了解某校七年级(3)班的全体学生鞋子的尺码情况 | |
| B. | 了解河北卫视《看今朝》栏目的收视率 | |
| C. | 调查品牌牛奶的质量情况 | |
| D. | 调查磨山市居民的人均收入的情况 |
3.若关于x的不等式组$\left\{\begin{array}{l}{x-a>0}\\{\frac{3x-1}{5}<1}\end{array}\right.$无解,则a的取值范围是( )
| A. | a>2 | B. | a≥2 | C. | 1<a≤2 | D. | 1≤a<2 |
20.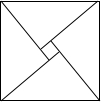 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示.如果大正方形的面积是l3,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2值为( )
2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示.如果大正方形的面积是l3,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2值为( )
 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示.如果大正方形的面积是l3,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2值为( )
2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示.如果大正方形的面积是l3,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2值为( )| A. | 25 | B. | 9 | C. | 13 | D. | 169 |
7.下列各组数中,以它们为边长的线段不能构成直角三角形的是( )
| A. | 3,4,5 | B. | 7,24,25 | C. | 1,$\sqrt{2}$,$\sqrt{3}$ | D. | 2,3,4 |
4.已知0<a<3,则点P(a-3,a)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.如图图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |