题目内容
10．
如图，把一块三角板的直角顶点放在直尺的一边上，如果∠1=30°，那么∠2为（ ）| A． | 60° | B． | 30° | C． | 70° | D． | 50° |
分析 由∠ACB=90°，∠1=30°，即可求得∠3的度数，又由a∥b，根据两直线平行，同位角相等，即可求得∠2的度数．
解答 
解：如图．
∵∠ACB=90°，∠1=30°，
∴∠3=∠ACB-∠1=90°-30°=60°，
∵a∥b，
∴∠2=∠3=60°．
故选A．
点评 此题考查了平行线的性质．此题比较简单，解题的关键是注意掌握两直线平行，同位角相等定理的应用．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
20．如图1，A、B、C是三个垃圾存放点，点B、C分别位于点A的正北和正东方向，AC=100米，四人分别测得∠C的度数如表：
他们又调查了各点的垃圾量，并绘制了下列尚不完整的统计图2，图3：
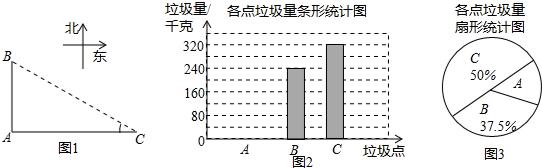
（1）求表中∠C度数的平均数$\overline{x}$；
（2）求A处的垃圾量，并将不完整的统计图2、3补充完整；
（3）用（1）中的$\overline{x}$作为∠C的度数，要将A处的垃圾沿道路AB都运到B处，已知运送1千克垃圾每米的费用为0.005元，求运垃圾所需的费用．
（注：sin37°=0.6，cos37°=0.8，tan37°=0.75）
| 甲 | 乙 | 丙 | 丁 | |
| ∠C（单位：度） | 34 | 36 | 38 | 40 |
（1）求表中∠C度数的平均数$\overline{x}$；
（2）求A处的垃圾量，并将不完整的统计图2、3补充完整；
（3）用（1）中的$\overline{x}$作为∠C的度数，要将A处的垃圾沿道路AB都运到B处，已知运送1千克垃圾每米的费用为0.005元，求运垃圾所需的费用．
（注：sin37°=0.6，cos37°=0.8，tan37°=0.75）
18．下列调查中，适合采用抽样调查的是（ ）
| A． | 对乘坐某班次飞机的乘客进行安检 | |
| B． | 了解一批节能灯管的使用寿命 | |
| C． | 选出某班学生中跑的最快的学生参加全县比赛 | |
| D． | 了解一班同学的视力情况 |
如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于G，下列结论：①BE=DF；②∠DAF=15°，③AC垂直平分EF，④BE+DF=EF，⑤S△AEC=S△ABC，其中正确结论有（ ）个．
2．下列根式中，属于最简二次根式的是（ ）
| A． | $\sqrt{5x}$ | B． | $\sqrt{0.5}$ | C． | $\sqrt{3{x}^{2}}$ | D． | $\sqrt{8}$ |
19．
如图，将周长为10cm的△ABC沿射线BC方向平移lcm后得到△DEF，则四边形ABFD的周长为（ ）
如图，将周长为10cm的△ABC沿射线BC方向平移lcm后得到△DEF，则四边形ABFD的周长为（ ）| A． | 11cm | B． | 12cm | C． | 13cm | D． | 14cm |
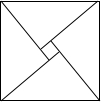2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图，它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形，如图所示．如果大正方形的面积是l3，小正方形的面积是1，直角三角形的较短直角边长为a，较长直角边长为b，那么（a+b）2值为（ ）