题目内容
10.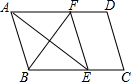 如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )
如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
分析 先证明四边形ABEF是平行四边形,再证明邻边相等即可得出四边形ABEF是菱形,得出AE⊥BF,OA=OE,OB=OF=$\frac{1}{2}$BF=6,由勾股定理求出OA,即可得出AE的长.
解答 解:如图所示:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵∠BAD的平分线交BC于点E,
∴∠DAE=∠BAE,
∴∠BAE=∠BEA,
∴AB=BE,同理可得AB=AF,
∴AF=BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形,
∴AE⊥BF,OA=OE,OB=OF=$\frac{1}{2}$BF=6,
∴OA=$\sqrt{A{B}^{2}-O{B}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴AE=2OA=16;
故选:D.
点评 本题考查平行四边形的性质与判定、等腰三角形的判定、菱形的判定和性质、勾股定理等知识;熟练掌握平行四边形的性质,证明四边形ABEF是菱形是解决问题的关键.

练习册系列答案
相关题目
20.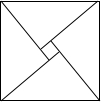 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示.如果大正方形的面积是l3,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2值为( )
2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示.如果大正方形的面积是l3,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2值为( )
 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示.如果大正方形的面积是l3,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2值为( )
2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示.如果大正方形的面积是l3,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2值为( )| A. | 25 | B. | 9 | C. | 13 | D. | 169 |
5.如图图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
2. 如图,BC∥DE,AB∥CD,∠B=40°,则∠D的度数是( )
如图,BC∥DE,AB∥CD,∠B=40°,则∠D的度数是( )
 如图,BC∥DE,AB∥CD,∠B=40°,则∠D的度数是( )
如图,BC∥DE,AB∥CD,∠B=40°,则∠D的度数是( )| A. | 40° | B. | 100° | C. | 120° | D. | 140° |
19.-$\root{3}{-64}$的平方根是( )
| A. | 2 | B. | ±2 | C. | ±4 | D. | 不存在 |
1.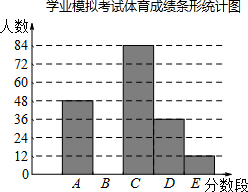 为迎接2016年贵阳市初中毕业生学业体育考试,某校进行了九年级学生学业考试体育模拟考试.为了解本次模拟考试的成绩(分数为整数)情况,现从中随机抽取部分学生的体育成绩分为五个等级,其中A:50分;B:49-45分;C:44-40分;D:39-30分;E:29-0分.根据所分等级情况制作了如下两个不完整的统计图表:
为迎接2016年贵阳市初中毕业生学业体育考试,某校进行了九年级学生学业考试体育模拟考试.为了解本次模拟考试的成绩(分数为整数)情况,现从中随机抽取部分学生的体育成绩分为五个等级,其中A:50分;B:49-45分;C:44-40分;D:39-30分;E:29-0分.根据所分等级情况制作了如下两个不完整的统计图表:
学业模拟专试体育成绩(分数段)
根据图表提供的信息,回答下列问题:
(1)在统计表中,m的值为60,n的值为0.15;
(2)将统计图补充完整;
(3)如果把成绩在30分以上(含30分)定为合格,那么估计该校今年1600名九年级学生中体育成绩为合格的学生人数约有多少人?
 为迎接2016年贵阳市初中毕业生学业体育考试,某校进行了九年级学生学业考试体育模拟考试.为了解本次模拟考试的成绩(分数为整数)情况,现从中随机抽取部分学生的体育成绩分为五个等级,其中A:50分;B:49-45分;C:44-40分;D:39-30分;E:29-0分.根据所分等级情况制作了如下两个不完整的统计图表:
为迎接2016年贵阳市初中毕业生学业体育考试,某校进行了九年级学生学业考试体育模拟考试.为了解本次模拟考试的成绩(分数为整数)情况,现从中随机抽取部分学生的体育成绩分为五个等级,其中A:50分;B:49-45分;C:44-40分;D:39-30分;E:29-0分.根据所分等级情况制作了如下两个不完整的统计图表:学业模拟专试体育成绩(分数段)
| 分数段 | 人数/人 | 频数 |
| A | 48 | 0.2 |
| B | m | 0.25 |
| C | 84 | 0.35 |
| D | 36 | n |
| E | 12 | 0.05 |
(1)在统计表中,m的值为60,n的值为0.15;
(2)将统计图补充完整;
(3)如果把成绩在30分以上(含30分)定为合格,那么估计该校今年1600名九年级学生中体育成绩为合格的学生人数约有多少人?
 如图,一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人形通道.
如图,一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人形通道. 据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m)
据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m)