题目内容
在5×5的方格棋盘内的一个格中填入一个数-1,其余的格填1,每次操作是任取一个k×k的正方形(2≤k≤5),将其中的所有数都变号,问:-1填入哪一格才能通过适当的有限次操作,使棋盘中所有数都变为1?
考点:染色问题
专题:
分析:先根据题意得出含有偶数个黑色格,再根据黑格内各数的积不变,始终为-1,得出黑格中至少有一个为-1,不可能全都变为1,从而得出黑格都不能填-1,再将图形进行旋转90°,180°,270°,即可得出1填入哪一格才能通过适当的有限次操作;再把-1填入中心方格放,先取左上的3×3和右下的3×3正方形进行操作,或先取左下的2×2和右上的2×2正方形进行操作,最后取全部的5×5正方形进行操作即可得出答案.
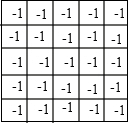
解答: 解:将5×5的棋盘按如图所示的若干个格染成黑色,对任何一个k×k(2≤k≤5)的正方形,必含有偶数个黑色格,
解:将5×5的棋盘按如图所示的若干个格染成黑色,对任何一个k×k(2≤k≤5)的正方形,必含有偶数个黑色格,
如果将最初的-1填入黑色格中,那么每次改变偶数个黑格的符号,从而黑格内各数的积不变,始终为-1,
从而黑格中至少有一个-1,不可能全都变为1,于是,所有黑格都不能填-1,
将上述图形进行旋转90°,180°,270°,得到另外的黑格集,-1也不能放如这些黑格中,这些黑格集包含了除中心外的所有方格,
故-1最多放在中心这一方格中.
当中心方格放-1时,先取左上的3×3正方形进行操作,再取右下的3×3正方形进行操作,又先取左下的2×2正方形进行操作,再取右上的2×2正方形进行操作,最后取全部的5×5正方形进行操作即可,使所有数都变为1.
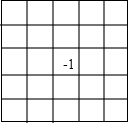




 解:将5×5的棋盘按如图所示的若干个格染成黑色,对任何一个k×k(2≤k≤5)的正方形,必含有偶数个黑色格,
解:将5×5的棋盘按如图所示的若干个格染成黑色,对任何一个k×k(2≤k≤5)的正方形,必含有偶数个黑色格,如果将最初的-1填入黑色格中,那么每次改变偶数个黑格的符号,从而黑格内各数的积不变,始终为-1,
从而黑格中至少有一个-1,不可能全都变为1,于是,所有黑格都不能填-1,
将上述图形进行旋转90°,180°,270°,得到另外的黑格集,-1也不能放如这些黑格中,这些黑格集包含了除中心外的所有方格,
故-1最多放在中心这一方格中.
当中心方格放-1时,先取左上的3×3正方形进行操作,再取右下的3×3正方形进行操作,又先取左下的2×2正方形进行操作,再取右上的2×2正方形进行操作,最后取全部的5×5正方形进行操作即可,使所有数都变为1.






点评:此题考查了染色问题,解题的关键是推断出-1所在的位置,并画出图形,主要考查了学生的想象能力,难度有点大,解题思路不是很容易想出,做题时要细心.

练习册系列答案
相关题目
圆周上共有10个等分点,以其中三点为顶点的直角三角形的个数为( )
| A、20 | B、40 | C、60 | D、80 |
魔术大师在表演魔术,他向观众出示一个盒子,内有10个小球,接着他从中任取一些小球,把每一个小球都变成8个小球,将其放回盒中,他不断地从盒中取一些小球,把每一个小球都变成8个小球后放回盒中,如此进行,到某一时刻,魔术师停止变魔术时,盒中球的总数可以是下面的( )
| A、2002 | B、2003 |
| C、2004 | D、2005 |
锐角三角形△ABC中,∠C=2∠B,则∠B的范围是( )
| A、10°<∠B<20° |
| B、20°<∠B<30° |
| C、30°<∠B<45° |
| D、45°<∠B<60° |