Question

凸四边形ABCD的面积是S，四边形内一点M关于四边中点的对称点分别是P、Q、R、S，则四边形PQRS的面积是

 

．

Answer 1

考点：面积及等积变换

专题：

分析：首先利用相似三角形的性质得出

S△AWR

S△ADB

=(

1

2

) 2=

1

4

，进而得出S_{四边形RWVX}=

1

2

S_{四边形ABCD}，再利用边之间关系得出

S△RMX

S△PMQ

=(

1

2

) 2=

1

4

，以及

S△MRW

S△MPS

=

S △MWV

S△MSR

=

S△MVX

S△MRQ

=

1

4

，可得S_{四边形RWVX}=

1

4

S_{四边形PSRQ}，即可得出2S_{四边形ABCD}=S_{四边形PSRQ}，即可得出答案．

解答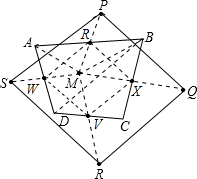：解：设该凸四边形为四边形ABCD，不妨设M关于AB、BC、CD、DA的中点对称的点分别是P、Q、R、S，
设AB，BC，CD，AD的中点分别为：R，X，V，W，连接RX，WR，XV，WV，BD，
∵W是AD中点，R是AB中点，
∴WR∥BD，WR=

1

2

BD，
∴△AWR∽△ADB，
∴

S△AWR

S△ADB

=(

1

2

) 2=

1

4

，
同理可得：

S△CVX

S△CDB

=

1

4

，
∴S_△AWR+S_△CVX=

1

4

S_{四边形ABCD}，
同理可得：S_{四边形RWVX}=

1

2

S_{四边形ABCD}，
∵R，W，V，X还是PM，SM，MR，MQ的中点，
∴RX∥PQ，RX=

1

2

PQ；RW∥PS，RW=

1

2

PS；VW∥RS，VW=

1

2

SR；VX∥RQ，VX=

1

2

QR，
∴

S△RMX

S△PMQ

=(

1

2

) 2=

1

4

，
同理可得出：

S△MRW

S△MPS

=

S △MWV

S△MSR

=

S△MVX

S△MRQ

=

1

4

，
故S_{四边形RWVX}=

1

4

S_{四边形PSRQ}，
进而得出：

1

4

S_{四边形PSRQ}=

1

2

S_{四边形ABCD}，
∴2S_{四边形ABCD}=S_{四边形PSRQ}，
∵凸四边形ABCD的面积是S，
∴S_{四边形PSRQ}=2S．
故答案为：2S．

点评：此题主要考查了相似三角形的性质以及面积的等积变换，利用相似三角形的性质得出S_{四边形RWVX}=

1

2

S_{四边形ABCD}和S_{四边形RWVX}=

1

4

S_{四边形PSRQ}是解题关键．