题目内容
以方程2x2-3x-2=0的两个根为横纵坐标的点,既在正比例函数y=k1x(k1≠0)的图象上,又在反比例函数y=
(k2≠0)的图象上,则k1•k2= .
| k2 |
| x |
考点:反比例函数与一次函数的交点问题,解一元二次方程-因式分解法
专题:
分析:首先求出方程2x2-3x-2=0的解,从而得到既在正比例函数y=k1x(k1≠0)的图象上,又在反比例函数y=
(k2≠0)的图象上的点的坐标,再利用待定系数法把点的坐标分别代入两个函数关系式中,从而求出k1、k2的值,再求积即可.
| k2 |
| x |
解答:解:∵方程2x2-3x-2=0的解为:x1=2,x2=-
,
∴点的坐标为:(2,-
)或(-
,2),
①当(2,-
)既在正比例函数y=k1x(k1≠0)的图象上,又在反比例函数y=
(k2≠0)的图象上时,
k1=
=
=-
,k2=xy=2×(-
)=-1,
则k1•k2=
;
②当(-
,2)既在正比例函数y=k1x(k1≠0)的图象上,又在反比例函数y=
(k2≠0)的图象上时,
k1=
=
=-4,k2=xy=-
×2=-1,
则k1•k2=-1×(-4)=4,;
故答案为:4或
.
| 1 |
| 2 |
∴点的坐标为:(2,-
| 1 |
| 2 |
| 1 |
| 2 |
①当(2,-
| 1 |
| 2 |
| k2 |
| x |
k1=
| y |
| x |
-
| ||
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
则k1•k2=
| 1 |
| 4 |
②当(-
| 1 |
| 2 |
| k2 |
| x |
k1=
| y |
| x |
| 2 | ||
-
|
| 1 |
| 2 |
则k1•k2=-1×(-4)=4,;
故答案为:4或
| 1 |
| 4 |
点评:此题主要考查了解一元二次方程,以及待定系数法求函数关系式中的k的值,关键是求出在两个函数图象上的点的坐标,注意分情况讨论,考虑要全面.

练习册系列答案
相关题目
若x,y为实数,且|x-2|+(y+1)2=0,则
的值是( )
| x-y |
| A、1 | ||
| B、0 | ||
C、
| ||
D、
|
如果一个扇形的圆心角为120°,半径为4cm,则这个扇形的面积为( )cm2.
| A、π | ||
B、
| ||
C、
| ||
D、
|
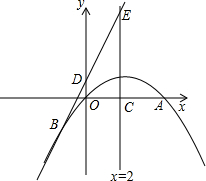 如图,已知二次函数y=ax2+bx+c的图象经过原点O和x轴上的另一点A,它的对称轴直线x=2与x轴交于点C,直线y=2x+1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于D、E.
如图,已知二次函数y=ax2+bx+c的图象经过原点O和x轴上的另一点A,它的对称轴直线x=2与x轴交于点C,直线y=2x+1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于D、E.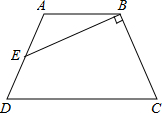 如图,已知等腰梯形ABCD中,AB∥CD,AB=2,CD=4,AD=BC,E是AD的中点,EB⊥BC,则梯形ABCD的面积是
如图,已知等腰梯形ABCD中,AB∥CD,AB=2,CD=4,AD=BC,E是AD的中点,EB⊥BC,则梯形ABCD的面积是