题目内容
在一条公路上汽车A、B、C分别以每小时80km,70km,50km的速度行驶.早上8时,汽车A、C从甲站开往乙站,同时,汽车B从乙站开往甲站,途中车B与车A相遇两个半小时后再与车C相遇,则甲、乙两站的距离是 km.
考点:一元一次方程的应用
专题:
分析:首先设甲、乙两站相距xkm,由题意可得等量关系为:B、C两人相遇所用的时间-A、B两人所用的时间=2
,根据等量关系可得方程:
-
=2
,再解方程即可.
| 1 |
| 2 |
| x |
| 70+50 |
| x |
| 80+70 |
| 1 |
| 2 |
解答:解:设甲、乙两站相距xkm,
-
=2
,
解得x=1500.
故答案为:1500.
| x |
| 70+50 |
| x |
| 80+70 |
| 1 |
| 2 |
解得x=1500.
故答案为:1500.
点评:考查一元一次方程在行程问题中的应用,关键是首先弄清题意,找到时间之间的关系,根据时间差列出方程,此题用到的公式是:时间=
.
| 路程 |
| 速度 |

练习册系列答案
相关题目
若abc=1,且
+
+
=2003.则x等于( )
| x |
| 1+a+ab |
| x |
| 1+b+bc |
| x |
| 1+c+ac |
| A、1 | B、2003 |
| C、4006 | D、2008 |
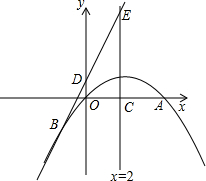 如图,已知二次函数y=ax2+bx+c的图象经过原点O和x轴上的另一点A,它的对称轴直线x=2与x轴交于点C,直线y=2x+1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于D、E.
如图,已知二次函数y=ax2+bx+c的图象经过原点O和x轴上的另一点A,它的对称轴直线x=2与x轴交于点C,直线y=2x+1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于D、E.