题目内容
已知直线y=4-x与x轴、y轴分别相交于C、D两点,有反比例函数y=
(m>0,x>0)的图象与之在同一坐标系.
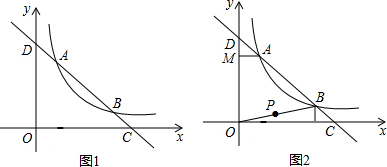
(1)若直线y=4-x与反比例函数图象相切,求m的值;
(2)如图1,若两图象相交于A、B两点,其中点A的横坐标为1,利用函数图象求关于x的不等式4-x<
的解集;
(3)在(2)的情况下,过点A向y轴作垂线AM,垂足为M,如图2,有一动点P从原点O出发沿O→B→A→M(BA段为曲线)的路线运动,点P的横坐标为a,由点p分别向x、y轴作垂线,垂足为E、F,四边形OEPF的面积为S,求S关于a的函数关系式.
| m |
| x |

(1)若直线y=4-x与反比例函数图象相切,求m的值;
(2)如图1,若两图象相交于A、B两点,其中点A的横坐标为1,利用函数图象求关于x的不等式4-x<
| m |
| x |
(3)在(2)的情况下,过点A向y轴作垂线AM,垂足为M,如图2,有一动点P从原点O出发沿O→B→A→M(BA段为曲线)的路线运动,点P的横坐标为a,由点p分别向x、y轴作垂线,垂足为E、F,四边形OEPF的面积为S,求S关于a的函数关系式.
考点:反比例函数综合题,根的判别式,待定系数法求一次函数解析式,待定系数法求反比例函数解析式,反比例函数与一次函数的交点问题,矩形的判定与性质
专题:综合题
分析:(1)若直线y=4-x与反比例函数y=
(m>0,x>0)的图象相切,则方程4-x=
即x2-4x+m=0有两个相等的实数根,则根的判别式等于0,从而可以求出m的值.
(2)由条件可依次求出点A的坐标、反比例函数的解析式、点B的坐标;设y1=4-x,y2=
,可将“求关于x的不等式4-x<
的解集”转化为“求函数y1的函数值小于函数y2的函数值时对应的自变量x的取值范围”,只需结合图象就可解决问题.
(3)设点P的坐标为(a,b),易证四边形OEPF是矩形,从而得到S=S矩形OEPF=OE•OF=ab.然后对点P分别在线段OB、双曲线上BA段、线段AM三个位置进行讨论,即可求出对应的S关于a的函数关系式.
| m |
| x |
| m |
| x |
(2)由条件可依次求出点A的坐标、反比例函数的解析式、点B的坐标;设y1=4-x,y2=
| m |
| x |
| m |
| x |
(3)设点P的坐标为(a,b),易证四边形OEPF是矩形,从而得到S=S矩形OEPF=OE•OF=ab.然后对点P分别在线段OB、双曲线上BA段、线段AM三个位置进行讨论,即可求出对应的S关于a的函数关系式.
解答:解:(1)若直线y=4-x与反比例函数y=
的图象相切,
则方程4-x=
即方程x2-4x+m=0有两个相等的实数根,
则(-4)2-4×1×m=0.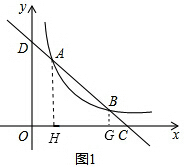
∴m=4.
(2)过点A作AH⊥x轴,垂足为H,点B作BG⊥x轴,垂足为G,如图1,
∵点A在直线y=4-x上,且xA=1,
∴yA=4-1=3.
∴点A的坐标为(1,3).
∴xH=1.
∵点A(1,3)在反比例函数y=
图象上,
∴m=1×3=3.
∴反比例函数的解析式为y=
.
联立
,
解得:
或
.
∴点B的坐标为(3,1).
∴xG=3.
设y1=4-x,y2=
(m>0,x>0),
结合图象可得:
当0<x<1或x>3时,y1<y2,即4-x<
.
∴关于x的不等式4-x<
的解集为0<x<1或x>3.
(3)设点P的坐标为(a,b),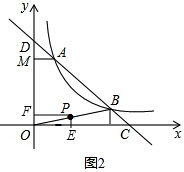
∵点P在第一象限,
∴OE=a,OF=b.
∵PE⊥x轴,PF⊥y轴,OE⊥OF,
∴∠EOF=∠OEP=∠OFP=90°.
∴四边形OEPF是矩形.
∴S=S矩形OEPF=OE•OF=ab.
①当点P在线段OB上时,如图2,
设OB的解析式为y=kx,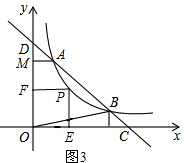
∵点B的坐标为(3,1)
∴3k=1.
∴k=
.
∴OB的解析式为y=
x.
∵点P在线段OB上,
∴b=
a.
∴S=ab=
a2.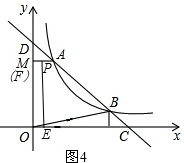
②当点P在双曲线y=
上时,如图3,
则有ab=3.
∴S=ab=3.
③当点P在线段AM上时,如图4,
此时b=3.
∴S=ab=3a.
综上所述:当点P在线段OB上时,S=
a2;当点P在双曲线上时,S=3;当点P在线段AM上时,S=3a.
| m |
| x |
则方程4-x=
| m |
| x |
则(-4)2-4×1×m=0.

∴m=4.
(2)过点A作AH⊥x轴,垂足为H,点B作BG⊥x轴,垂足为G,如图1,
∵点A在直线y=4-x上,且xA=1,
∴yA=4-1=3.
∴点A的坐标为(1,3).
∴xH=1.
∵点A(1,3)在反比例函数y=
| m |
| x |
∴m=1×3=3.
∴反比例函数的解析式为y=
| 3 |
| x |
联立
|
解得:
|
|
∴点B的坐标为(3,1).
∴xG=3.
设y1=4-x,y2=
| m |
| x |
结合图象可得:
当0<x<1或x>3时,y1<y2,即4-x<
| m |
| x |
∴关于x的不等式4-x<
| m |
| x |
(3)设点P的坐标为(a,b),

∵点P在第一象限,
∴OE=a,OF=b.
∵PE⊥x轴,PF⊥y轴,OE⊥OF,
∴∠EOF=∠OEP=∠OFP=90°.
∴四边形OEPF是矩形.
∴S=S矩形OEPF=OE•OF=ab.
①当点P在线段OB上时,如图2,
设OB的解析式为y=kx,

∵点B的坐标为(3,1)
∴3k=1.
∴k=
| 1 |
| 3 |
∴OB的解析式为y=
| 1 |
| 3 |
∵点P在线段OB上,
∴b=
| 1 |
| 3 |
∴S=ab=
| 1 |
| 3 |

②当点P在双曲线y=
| 3 |
| x |
则有ab=3.
∴S=ab=3.
③当点P在线段AM上时,如图4,
此时b=3.
∴S=ab=3a.
综上所述:当点P在线段OB上时,S=
| 1 |
| 3 |
点评:本题考查了双曲线与直线的交点问题,考查了用待定系数法求反比例函数及一次函数的解析式、矩形的判定与性质、根的判别式等知识,考查了数形结合以及分类讨论的思想,是一道好题.

练习册系列答案
相关题目
 我市某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是170cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材.如图1,(单位:cm)
我市某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是170cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材.如图1,(单位:cm)
 如图,直线AB、CD、EF相交于点O,OG平分∠COF,∠1=30°,∠2=45°.求∠3的度数.
如图,直线AB、CD、EF相交于点O,OG平分∠COF,∠1=30°,∠2=45°.求∠3的度数.