题目内容
某学校准备购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买2个足球和3个篮球共需340元,购买5个足球和2个篮球共需410元.
(1)购买一个足球、一个篮球各需多少元?
(2)根据学校的实际情况,需购买足球和篮球共96个,并且总费用不超过5720元.问最多可以购买多少个篮球?
(1)购买一个足球、一个篮球各需多少元?
(2)根据学校的实际情况,需购买足球和篮球共96个,并且总费用不超过5720元.问最多可以购买多少个篮球?
考点:二元一次方程组的应用
专题:
分析:(1)设购买一个足球需要x元,购买一个篮球需要y元,根据购买2个足球和3个篮球共需340元,购买5个足球和2个篮球共需410元,列方程组求解;
(2)设购买a个篮球,则购买(96-a)个足球,根据总费用不超过5720元,列不等式求出最大整数解.
(2)设购买a个篮球,则购买(96-a)个足球,根据总费用不超过5720元,列不等式求出最大整数解.
解答:解:(1)设购买一个足球需要x元,购买一个篮球需要y元,
根据题意得:
,
解得:
,
答:购买一个足球需要50元,购买一个篮球需要80元;
(2)设购买a个篮球,则购买(96-a)个足球,
根据题意得:80a+50(96-a)≤5720,
解得:a≤
,
∵a是整数,
∴a≤30,
答:最多可以购买30个篮球.
根据题意得:
|
解得:
|
答:购买一个足球需要50元,购买一个篮球需要80元;
(2)设购买a个篮球,则购买(96-a)个足球,
根据题意得:80a+50(96-a)≤5720,
解得:a≤
| 92 |
| 3 |
∵a是整数,
∴a≤30,
答:最多可以购买30个篮球.
点评:本题考查了二元一次方程组的应用和一元一次不等式的应用,解答本题的关键是读懂题意,找出合适的等量关系和不等关系,列方程和不等式求解.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
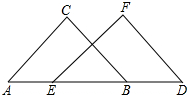 如图,AC∥EF,AC=EF,AE=BD,△ABC与△EDF全等吗?BC∥DF吗?请说明理由.
如图,AC∥EF,AC=EF,AE=BD,△ABC与△EDF全等吗?BC∥DF吗?请说明理由.