题目内容
1.观察下列算式,你发现了什么规律?13=$\frac{1×4}{4};{1^3}+{2^3}=\frac{4×9}{4};{1^3}+{2^3}+{3^3}=\frac{9×16}{4};{1^3}+{2^3}+{3^3}+{4^3}=\frac{16×25}{4}$;…
(1)根据你发现的规律,计算下面算式的值:13+23+33+…+83=$\frac{64×81}{4}$;
(2)请用一个含n的算式表示这个规律:13+23+33+…+n3=$\frac{{{n^2}{{({n+1})}^2}}}{4}$.
分析 (1)几个连续自然数的立方和其结果分母都为4,如果等号左边有1个加数,那么分子中的第一个因数为12,第二个因数为22,如果等号左边有2个加数,那么分子中的第一个因数为22,第二个因数为32,如果等号左边有n个加数,那么分子中的第一个因数为n2,第二个因数为(2n+1);
(2)根据规律得到:13+23+33+…+n3=$\frac{{{n^2}{{({n+1})}^2}}}{4}$.
解答 解:(1)根据发现的规律,计算下面算式的值:13+23+33+…+83=$\frac{64×81}{4}$;
(2)根据规律:13+23+33+…+n3=$\frac{{{n^2}{{({n+1})}^2}}}{4}$.
故答案为$\frac{64×81}{4}$;$\frac{{{n^2}{{({n+1})}^2}}}{4}$.
点评 考查数字的变化规律,解决此类探究性问题,关键在观察、分析已知数据,寻找它们之间的相互联系,探寻其规律.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
6.下面四个式子中正确的是( )
| A. | -$\frac{1}{5}$<-5<5 | B. | 5<-5<-$\frac{1}{5}$ | C. | -5<5<-$\frac{1}{5}$ | D. | -5<-$\frac{1}{5}$<5 |
10.在下列图案中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
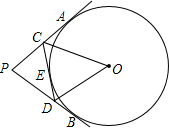 如图,PA,PB切⊙O于点A,B,点E是劣弧$\widehat{AB}$上一点,过E点作⊙O的切线交PA与C,交PB于D,若∠P=80°,∠DOC=50°.
如图,PA,PB切⊙O于点A,B,点E是劣弧$\widehat{AB}$上一点,过E点作⊙O的切线交PA与C,交PB于D,若∠P=80°,∠DOC=50°.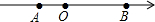 已知数轴上A,B对应的实数为a,b,化简代数式:|a-b|-$\sqrt{(b-a)^{2}}$+$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$=b-a.
已知数轴上A,B对应的实数为a,b,化简代数式:|a-b|-$\sqrt{(b-a)^{2}}$+$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$=b-a.