题目内容
11.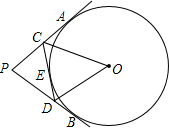 如图,PA,PB切⊙O于点A,B,点E是劣弧$\widehat{AB}$上一点,过E点作⊙O的切线交PA与C,交PB于D,若∠P=80°,∠DOC=50°.
如图,PA,PB切⊙O于点A,B,点E是劣弧$\widehat{AB}$上一点,过E点作⊙O的切线交PA与C,交PB于D,若∠P=80°,∠DOC=50°.
分析 连接OA、OE、OB,先证明OA⊥AP、OB⊥PB,从而得到∠P+∠AOB=180°,于是可求得∠AOB=100°,然后证明Rt△AOC≌Rt△EOC,得到∠AOC=∠COE同理可证明∠DOE=∠BOD,从而得到∠COD=$\frac{1}{2}$∠AOB.
解答 解:连接OB、OA、OE.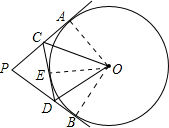
∵PA,PB切⊙O于点A,B,
∴∠OAP=∠OBP=90°.
∴∠P+∠AOB=180°.
∴∠AOB=180°-80°=100°.
∵DC是圆O的切线,
∴∠OEC=90°.
在Rt△AOC和Rt△EOC中,
$\left\{\begin{array}{l}{OA=OE}\\{OC=OC}\end{array}\right.$,
∴Rt△AOC≌Rt△EOC(HL).
∴∠AOC=∠COE.
同理:∠DOE=∠BOD.
∴∠COD=$\frac{1}{2}$∠AOB=50°.
故答案为:50°.
点评 本题主要考查的是切线的性质、全等三角形的性质和判定,求得∠COD=$\frac{1}{2}$∠AOB是解题的关键.

练习册系列答案
相关题目
16.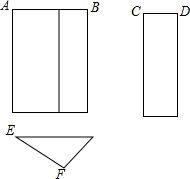 如图是一个三棱柱的三视图,若AB=5,CD=2,则EF的长度不可能是( )
如图是一个三棱柱的三视图,若AB=5,CD=2,则EF的长度不可能是( )
 如图是一个三棱柱的三视图,若AB=5,CD=2,则EF的长度不可能是( )
如图是一个三棱柱的三视图,若AB=5,CD=2,则EF的长度不可能是( )| A. | 4 | B. | 4.5 | C. | 5 | D. | 6 |
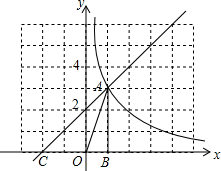 如图,在平面直角坐标系中,直线y=x+$\frac{1}{2}m$的图象与反比例函数y=$\frac{m}{x}$的图象在第一象限内交于点A,与x轴交于点C,AB垂直于X轴,垂足为B,且三角形AOB的面积为1.
如图,在平面直角坐标系中,直线y=x+$\frac{1}{2}m$的图象与反比例函数y=$\frac{m}{x}$的图象在第一象限内交于点A,与x轴交于点C,AB垂直于X轴,垂足为B,且三角形AOB的面积为1.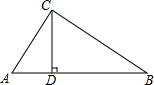 在Rt△ABC中,∠C=90°,CD是斜边AB的高.已知CD=5,sinB=$\frac{1}{3}$.求BC、BD、AD、AC的长以及tanA、cos∠ACD的值.
在Rt△ABC中,∠C=90°,CD是斜边AB的高.已知CD=5,sinB=$\frac{1}{3}$.求BC、BD、AD、AC的长以及tanA、cos∠ACD的值.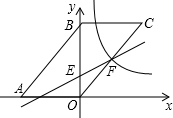 如图,在平面直角坐标系中,四边形ABCO是平行四边形,A点坐标(-6,0),B点坐标(0,6),点C在第一象限,直线y=$\frac{1}{2}$x+2与y轴交与点E,与OC交与点F,反比例函数y=$\frac{k}{x}$(x>0)经过点F.
如图,在平面直角坐标系中,四边形ABCO是平行四边形,A点坐标(-6,0),B点坐标(0,6),点C在第一象限,直线y=$\frac{1}{2}$x+2与y轴交与点E,与OC交与点F,反比例函数y=$\frac{k}{x}$(x>0)经过点F.