题目内容
12．已知当x1=a、x2=b、x3=c时，二次函数y=$\frac{1}{2}$x2+mx对应的函数值分别为y1、y2、y3，正整数a、b、c恰好是一个三角形的三边长，且当a＜b＜c时，都有y1＜y2＜y3，则a、b、c和的最小值为9，实数m的取值范围是m＞-2.5．分析 根据三角形的任意两边之和大于第三边判断出a最小为2，再根据二次函数的增减性和对称性判断出对称轴在2、3之间偏向2，即小于2.5，然后列出不等式求解即可．
解答 解：∵正整数a、b、c恰好是一个三角形的三边长，且当a＜b＜c，
∴a＞c-b≥1．
∴a＞1．
∴a、b、c的最小值分别为2、3、4．
∴a、b、c和的最小值为9．
故答案是：9；
（2）：∵正整数a，b，c恰好是一个三角形的三边长，且a＜b＜c，
∴a最小是2，b最小是3，
∴根据二次函数的增减性和对称性知，二次函数y=$\frac{1}{2}$x2+2mx的对称轴在2，3之间，且偏向2．
∵y1＜y2＜y3，
∴-$\frac{m}{2×\frac{1}{2}}$＜2.5，
解得m＞-2.5．
故答案为：m＞-2.5．
点评 本题考查了二次函数图象上点的坐标特征，三角形的三边关系，判断出a最小可以取2以及对称轴的位置是解题的关键．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
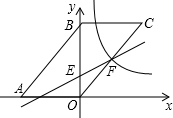如图，在平面直角坐标系中，四边形ABCO是平行四边形，A点坐标（-6，0），B点坐标（0，6），点C在第一象限，直线y=$\frac{1}{2}$x+2与y轴交与点E，与OC交与点F，反比例函数y=$\frac{k}{x}$（x＞0）经过点F．
7．抛物线y=-2（x-4）2+5的开口方向、对称轴、顶点坐标分别是（ ）
| A． | 向下、直线x=-4、（4，5） | B． | 向上、直线x=-4、（-4，5） | ||
| C． | 向下、直线x=4、（4，5） | D． | 向上、直线x=4、（-4，-5） |