题目内容
13. 已知,如图所示,在?ABCD中,∠BAD的平分线与BC交于E,∠ABC的平分线交AD于点F,AE,BF交于O,则四边形ABEF为菱形,请说明理由.
已知,如图所示,在?ABCD中,∠BAD的平分线与BC交于E,∠ABC的平分线交AD于点F,AE,BF交于O,则四边形ABEF为菱形,请说明理由.
分析 先证明四边形ABEF是平行四边形,再证明邻边相等即可得出结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵∠BAD的平分线交BC于点E,
∴∠DAE=∠BEA,
∴∠BAE=∠BEA,
∴AB=BE,
同理:AB=AF,
∴AF=BE,
∵AF∥BE,
∴四边形ABEF是平行四边形,
∵AB=AF
∴四边形ABEF是菱形.
点评 本题考查平行四边形的性质、菱形的判定;熟练掌握平行四边形的性质,证明AB=BE=AF是解决问题的关键.

练习册系列答案
相关题目
1. 如图,在点O处测得远处动点P作匀速直线运动,开始位置在A点,一分钟后到达B点,再过一分钟到达C点,测得∠AOB=90°,∠BOC=30°,则tan∠OAB=( )
如图,在点O处测得远处动点P作匀速直线运动,开始位置在A点,一分钟后到达B点,再过一分钟到达C点,测得∠AOB=90°,∠BOC=30°,则tan∠OAB=( )
 如图,在点O处测得远处动点P作匀速直线运动,开始位置在A点,一分钟后到达B点,再过一分钟到达C点,测得∠AOB=90°,∠BOC=30°,则tan∠OAB=( )
如图,在点O处测得远处动点P作匀速直线运动,开始位置在A点,一分钟后到达B点,再过一分钟到达C点,测得∠AOB=90°,∠BOC=30°,则tan∠OAB=( )| A. | $\frac{3}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{2}{3}$ |
2.点D、E、F分别在△ABC的三边BC、AB、AC上,且AD、BF、CE相交于一点M,若$\frac{AB}{BE}+\frac{AC}{CF}=5$,则$\frac{AM}{MD}$=( )
| A. | $\frac{7}{2}$ | B. | 3 | C. | $\frac{5}{2}$ | D. | 2 |
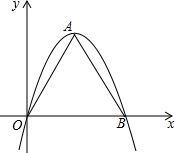 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
 如图,AD与BC交于点E,∠BAC=∠ACD=90°,∠B=45°,∠D=30°,则$\frac{BE}{EC}$的值是$\frac{\sqrt{3}}{3}$.
如图,AD与BC交于点E,∠BAC=∠ACD=90°,∠B=45°,∠D=30°,则$\frac{BE}{EC}$的值是$\frac{\sqrt{3}}{3}$.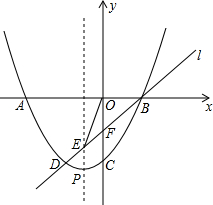 如图,已知二次函数y=ax2+2ax+c(a>0)的图象交x轴于A、B两点,交y轴于点C.过点B的直线l与这个二次函数的图象的另一个交点为D,与该图象的对称轴交于点E,与y轴交于点F,且DE:EF:FB=1:1:2.
如图,已知二次函数y=ax2+2ax+c(a>0)的图象交x轴于A、B两点,交y轴于点C.过点B的直线l与这个二次函数的图象的另一个交点为D,与该图象的对称轴交于点E,与y轴交于点F,且DE:EF:FB=1:1:2.