题目内容
1.如图,等边△ABC中,D是BC中点,过点D作DF⊥AC于点F,P在AB上,连DP,以DP为斜边作Rt△DPE,且∠EDP=∠B,连接EF.
(1)求证:AP=2EF;
(2)连接AE并延长交BC于点K,交DF于点H,若BP=8,PE:EF=$\sqrt{19}$:2时,求DH的长.
分析 (1)如图1,连接AD,由△ABC是等边三角形,得到∠B=∠C=60°,∠DAC=$\frac{1}{2}$∠BAC=30°,根据已知条件得到$\frac{PD}{DE}=\frac{AD}{DF}$=2,推出△APD∽△EDF,根据相似三角形的性质即可得到结论;
(2)如图2,连接AD,过P作PM⊥BC于M,设PE=$\sqrt{19}$k,EF=2k,于是得到AP=2EF=4k,求出AB=8+4k,解直角三角形得到PD=$\frac{2\sqrt{19}k}{\sqrt{3}}$,根据勾股定理列方程得到EF=$\frac{3}{2}$,CD=$\frac{11}{2}$,DF=$\frac{11}{4}$$\sqrt{3}$,根据相似三角形的性质得到$\frac{EF}{CK}=\frac{AF}{AC}$=$\frac{3}{4}$,$\frac{EF}{DK}=\frac{HF}{DH}$,代入数据即可得到结论.
解答 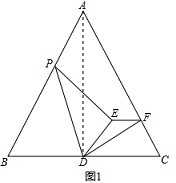 (1)证明:如图1,连接AD,
(1)证明:如图1,连接AD,
∵△ABC是等边三角形,
∴∠B=∠C=60°,∠DAC=$\frac{1}{2}$∠BAC=30°,
∵DF⊥AC,
∴AD=2DF,∠ADF=60°,
∵∠PDE=∠B=60°,
∴∠ADP=∠EDF,
∵∠PED=90°,
∴PD=2DE,
∴$\frac{PD}{DE}=\frac{AD}{DF}$=2,
∴△APD∽△EDF,
∴$\frac{AP}{EF}=\frac{AD}{DF}$=2,
∴AP=2EF;
(2)如图2,连接AD,过P作PM⊥BC于M,
∵PB=8,∴BM=4,PM=4$\sqrt{3}$,
∵PE:EF=$\sqrt{19}$:2,设PE=$\sqrt{19}$k,EF=2k,∴AP=2EF=4k,
∴AB=8+4k,
∴BD=CD=4+2k,
在Rt△PDE中,
∵∠DPE=30°,∠PED=90°,
∴PD=$\frac{2\sqrt{19}k}{\sqrt{3}}$,
∴DM2=PD2-PM2,
∵DM=BD-BM,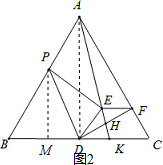
∴($\frac{2\sqrt{19}}{\sqrt{3}}$k)2-(2$\sqrt{3}$)2=(4+2k-4)2,
∴k=$\frac{3}{4}$,
∴EF=$\frac{3}{2}$,CD=$\frac{11}{2}$,∴DF=$\frac{11}{4}$$\sqrt{3}$,
∵△APD∽△EDF,
∴∠EFD=∠PAD=30°,
∴∠EFD=∠FDC,
∴EF∥CD,
∴△AEF∽△AKC,
∴$\frac{EF}{CK}=\frac{AF}{AC}$=$\frac{3}{4}$,
∴CK=2,
∴DK=$\frac{7}{2}$,
∵EF∥CD,
∴△HEF∽△DKH,
∴$\frac{EF}{DK}=\frac{HF}{DH}$,
∴$\frac{\frac{3}{2}}{\frac{7}{2}}=\frac{\frac{11\sqrt{3}}{4}-DH}{DH}$,
∴DH=$\frac{77\sqrt{3}}{40}$.
点评 本题考查了相似三角形的判定和性质,等边三角形的性质,勾股定理,平行线的判定和性质,正确的作出辅助线是解题的关键.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案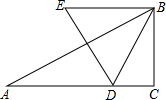 如图,已知△ABC,∠C=90°,∠A=30°,AC=$\sqrt{3}$,动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧),在点D从点A移动至点C的过程中,点E移动的路线为( )
如图,已知△ABC,∠C=90°,∠A=30°,AC=$\sqrt{3}$,动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧),在点D从点A移动至点C的过程中,点E移动的路线为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
 据国家教育部、卫生部最新调查表明:我国小学生近视率超过25%,初中生近视率达到70%,每年以8%的速度增长,居世界第一位.某市为调查中学生视力情况,从全市九年级学生中抽取了部分学生,统计了每个人连续三年视力检查的结果,并将所得数据处理后,制成统计表和扇形统计图如下:
据国家教育部、卫生部最新调查表明:我国小学生近视率超过25%,初中生近视率达到70%,每年以8%的速度增长,居世界第一位.某市为调查中学生视力情况,从全市九年级学生中抽取了部分学生,统计了每个人连续三年视力检查的结果,并将所得数据处理后,制成统计表和扇形统计图如下:被抽取学生视力在4.9以下的人数变化情况统计表
| 年份 | 2014 | 2015 | 2016 |
| 人数 | 300 | 500 | 800 |
(1)扇形统计图中x=10;
(2)该市共抽取了九年级学生2000名;
(3)若该市今年共有九年级学生约8.5万名,请你估计该市九年级学生视力不良(4.9以下)的学生大约有多少名?
| A. | m<$\frac{1}{3}$ | B. | m<-$\frac{1}{3}$ | C. | m>$\frac{1}{3}$ | D. | m>-$\frac{1}{3}$ |
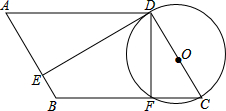 如图,四边形ABCD为平行四边形,以CD为直径作⊙O,⊙O与边BC相交于点F,⊙O的切线DE与边相交于点E,且AE=3EB.
如图,四边形ABCD为平行四边形,以CD为直径作⊙O,⊙O与边BC相交于点F,⊙O的切线DE与边相交于点E,且AE=3EB. 如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,AB=AE,BE的延长线分别交AD、AC的延长线于点F、G.
如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,AB=AE,BE的延长线分别交AD、AC的延长线于点F、G. 已知,如图所示,在?ABCD中,∠BAD的平分线与BC交于E,∠ABC的平分线交AD于点F,AE,BF交于O,则四边形ABEF为菱形,请说明理由.
已知,如图所示,在?ABCD中,∠BAD的平分线与BC交于E,∠ABC的平分线交AD于点F,AE,BF交于O,则四边形ABEF为菱形,请说明理由.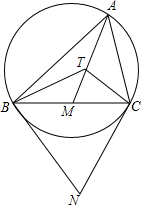 已知锐角△ABC及其外接圆,AM是边BC的中线,分别过点B,C作外接圆的切线,两条切线交于点N,T是AM上的一点,且∠ATC=∠ABN,求证:$\frac{AB}{AC}=\frac{TB}{TC}$.
已知锐角△ABC及其外接圆,AM是边BC的中线,分别过点B,C作外接圆的切线,两条切线交于点N,T是AM上的一点,且∠ATC=∠ABN,求证:$\frac{AB}{AC}=\frac{TB}{TC}$.