题目内容
3.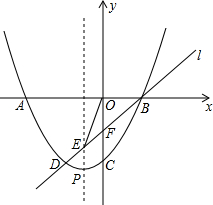 如图,已知二次函数y=ax2+2ax+c(a>0)的图象交x轴于A、B两点,交y轴于点C.过点B的直线l与这个二次函数的图象的另一个交点为D,与该图象的对称轴交于点E,与y轴交于点F,且DE:EF:FB=1:1:2.
如图,已知二次函数y=ax2+2ax+c(a>0)的图象交x轴于A、B两点,交y轴于点C.过点B的直线l与这个二次函数的图象的另一个交点为D,与该图象的对称轴交于点E,与y轴交于点F,且DE:EF:FB=1:1:2.(1)求证:点F为OC的中点;
(2)连接OE,若△OBE的面积为2,求这个二次函数的关系式;
(3)设这个二次函数的图象的顶点为P,问:以DF为直径的圆是否可能恰好经过点P?若可能,请求出此时二次函数的关系式;若不可能,请说明理由.
分析 (1)首先得出对称轴,再表示出D,C点坐标,再利用全等三角形的判定方法得出△DCF≌△BOF,进而求出答案;
(2)首先得出F点坐标,进而利用待定系数法求出直线BC的解析式,进而得出答案;
(3)由(1)可得F(0,$\frac{c}{2}$),E(-1,$\frac{3c}{4}$),再利用EP=DE,进而得出关于a,c的等式,进而求出答案.
解答 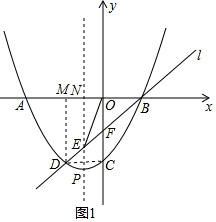 解:(1)如图1,过点D作DM∥FO,
解:(1)如图1,过点D作DM∥FO,
∵y=ax2+2ax+c=a(x+1)2+c-a,
∴它的对称轴为x=-1,
∵DE:EF:FB=1:1:2,且DM∥NE∥OF,
∴B(2,0),且D点的横坐标为-2,
由此可得D(-2,c),
∵点C(0,c),
∴D、C关于x=-1对称,
故∠DCF=90°,
在△DCF和△BOF中
$\left\{\begin{array}{l}{∠DFC=∠BFO}\\{∠DCF=∠FOB}\\{DC=OB}\end{array}\right.$,
∴△DCF≌△BOF,
∴OF=CF,
即点F为CO的中点.
(2)∵△OBE的面积为2,B(2,0),
∴E(-1,-2),
∵OF∥NE,
∴△BOF∽△BNE,
∴$\frac{FO}{EN}$=$\frac{BO}{BN}$,
∴$\frac{2}{3}$=$\frac{FO}{2}$,
解得:FO=$\frac{4}{3}$,
由此可得F(0,-$\frac{4}{3}$),C(0,-$\frac{8}{3}$),
把B(2,0),C(0,-$\frac{8}{3}$)代入y=ax2+2ax+c得
$\left\{\begin{array}{l}{4a+4a+c=0}\\{c=-\frac{8}{3}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{1}{3}}\\{c=-\frac{8}{3}}\end{array}\right.$.
∴抛物线解析式为:y=$\frac{1}{3}$x2+$\frac{2}{3}$x-$\frac{8}{3}$;
(3)以DF为直径的圆能够恰好经过点P,
由(1)可得F(0,$\frac{c}{2}$),E(-1,$\frac{3c}{4}$),D(-2,c),
∴DE=$\sqrt{(\frac{c}{4})^{2}+1}$,
要使以DF为直径的圆恰好经过点P,有EP=DE=$\sqrt{(\frac{c}{4})^{2}+1}$,
∵E(-1,$\frac{3c}{4}$),P(-1,c-a),
∴EP=$\frac{3}{4}$c-(c-a)=a-$\frac{1}{4}$c,
∴a-$\frac{1}{4}$c=$\sqrt{(\frac{c}{4})^{2}+1}$,
另一方面,由B(2,0)可得8a+c=0,即c=-8a,
把它代入上式可得a=$\frac{\sqrt{5}}{5}$,
∴y=$\frac{\sqrt{5}}{5}{x}^{2}+\frac{2\sqrt{5}}{5}$x-$\frac{8\sqrt{5}}{5}$.
点评 此题主要考查了二次函数综合以及相似三角形的判定与性质以及全等三角形的判定与性质等知识,正确表示出E,P点坐标是解题关键.

| A. | m<$\frac{1}{3}$ | B. | m<-$\frac{1}{3}$ | C. | m>$\frac{1}{3}$ | D. | m>-$\frac{1}{3}$ |
| A. | x5•x=x5 | B. | x5-x2=x3 | C. | (-y)2 (-y)7=y9 | D. | -y3•(-y)7=y10 |
 已知,如图所示,在?ABCD中,∠BAD的平分线与BC交于E,∠ABC的平分线交AD于点F,AE,BF交于O,则四边形ABEF为菱形,请说明理由.
已知,如图所示,在?ABCD中,∠BAD的平分线与BC交于E,∠ABC的平分线交AD于点F,AE,BF交于O,则四边形ABEF为菱形,请说明理由.
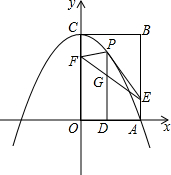 如图,边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A、C间的一个动点(含端点),过点P作PD⊥OA于点D,点E(8,2),F(0,6),连接PE、PF、EF.
如图,边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A、C间的一个动点(含端点),过点P作PD⊥OA于点D,点E(8,2),F(0,6),连接PE、PF、EF.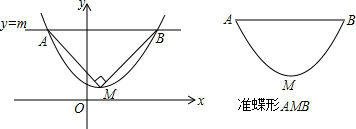
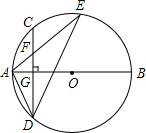 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3,给出下列结论:
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3,给出下列结论: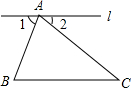 如图,点A在直线l上,如果∠B=75°,∠C=43°,若l∥BC,则∠BAC=62°.
如图,点A在直线l上,如果∠B=75°,∠C=43°,若l∥BC,则∠BAC=62°.