题目内容
2.点D、E、F分别在△ABC的三边BC、AB、AC上,且AD、BF、CE相交于一点M,若$\frac{AB}{BE}+\frac{AC}{CF}=5$,则$\frac{AM}{MD}$=( )| A. | $\frac{7}{2}$ | B. | 3 | C. | $\frac{5}{2}$ | D. | 2 |
分析 过A作PQ∥BC交BF的延长线于Q,交CE的延长线于P,根据全等三角形的性质得到$\frac{AF}{CF}=\frac{AQ}{BC},\frac{AE}{BE}=\frac{AP}{BC}$,根据比例的性质得到$\frac{AF+CF}{CF}=\frac{AQ+BC}{BC}$,$\frac{AE+BE}{BE}=\frac{AP+BC}{BC}$,两式相加得到$\frac{PQ+2BC}{BC}=5$,即可得到结论.
解答 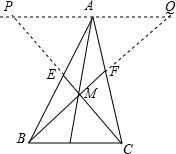 解:过A作PQ∥BC交BF的延长线于Q,交CE的延长线于P,
解:过A作PQ∥BC交BF的延长线于Q,交CE的延长线于P,
∴△AQF∽△BCF△APE∽△BCE,
∴$\frac{AF}{CF}=\frac{AQ}{BC},\frac{AE}{BE}=\frac{AP}{BC}$,
∴$\frac{AF+CF}{CF}=\frac{AQ+BC}{BC}$,$\frac{AE+BE}{BE}=\frac{AP+BC}{BC}$,
即$\frac{AC}{CF}=\frac{AQ+BC}{BC}$,$\frac{AB}{BE}=\frac{AP+BC}{BC}$,
∵$\frac{AC}{CF}+\frac{AB}{BE}=\frac{AQ+BC+AP+BC}{BC}=5$,
∴$\frac{PQ+2BC}{BC}=5$,
∴$\frac{AM}{MD}=\frac{QM}{BM}=\frac{PQ}{BC}$=3.
故选B.
点评 本题考查了相似三角形的判定和性质,比例的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
10.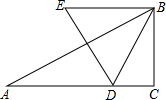 如图,已知△ABC,∠C=90°,∠A=30°,AC=$\sqrt{3}$,动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧),在点D从点A移动至点C的过程中,点E移动的路线为( )
如图,已知△ABC,∠C=90°,∠A=30°,AC=$\sqrt{3}$,动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧),在点D从点A移动至点C的过程中,点E移动的路线为( )
 如图,已知△ABC,∠C=90°,∠A=30°,AC=$\sqrt{3}$,动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧),在点D从点A移动至点C的过程中,点E移动的路线为( )
如图,已知△ABC,∠C=90°,∠A=30°,AC=$\sqrt{3}$,动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧),在点D从点A移动至点C的过程中,点E移动的路线为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
7. 某移动公司近日推出了如下两种月收费方式.
某移动公司近日推出了如下两种月收费方式.
已知k,l满足$\left\{\begin{array}{l}{2l-7k=1}\\{5k-l=10}\end{array}\right.$设每月的通话时间为x分钟,A、B两种收费方式的收费金额分别为yA元、yB元.
(I)求k,1的值.
(2)如图是yB与x之间的函数关系图象,请根据图象填空:m=10,n=50.
(3)写出yA与x之间的函数关系式.
(4)选择哪种收费方式较合算?为什么?
 某移动公司近日推出了如下两种月收费方式.
某移动公司近日推出了如下两种月收费方式.| 收费方式 | 月租费/元 | 赠送通话时间/分钟 | 超时费/(元/分钟) |
| A | k | l | 0.2 |
| B | m | n | 0.1 |
(I)求k,1的值.
(2)如图是yB与x之间的函数关系图象,请根据图象填空:m=10,n=50.
(3)写出yA与x之间的函数关系式.
(4)选择哪种收费方式较合算?为什么?
11.已知一次函数y=(1-3m)x+1,若y随x的增大而减小,则m的取值范围是( )
| A. | m<$\frac{1}{3}$ | B. | m<-$\frac{1}{3}$ | C. | m>$\frac{1}{3}$ | D. | m>-$\frac{1}{3}$ |
 已知,如图所示,在?ABCD中,∠BAD的平分线与BC交于E,∠ABC的平分线交AD于点F,AE,BF交于O,则四边形ABEF为菱形,请说明理由.
已知,如图所示,在?ABCD中,∠BAD的平分线与BC交于E,∠ABC的平分线交AD于点F,AE,BF交于O,则四边形ABEF为菱形,请说明理由.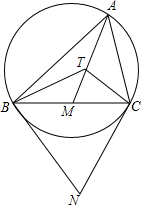 已知锐角△ABC及其外接圆,AM是边BC的中线,分别过点B,C作外接圆的切线,两条切线交于点N,T是AM上的一点,且∠ATC=∠ABN,求证:$\frac{AB}{AC}=\frac{TB}{TC}$.
已知锐角△ABC及其外接圆,AM是边BC的中线,分别过点B,C作外接圆的切线,两条切线交于点N,T是AM上的一点,且∠ATC=∠ABN,求证:$\frac{AB}{AC}=\frac{TB}{TC}$.
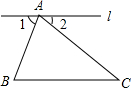 如图,点A在直线l上,如果∠B=75°,∠C=43°,若l∥BC,则∠BAC=62°.
如图,点A在直线l上,如果∠B=75°,∠C=43°,若l∥BC,则∠BAC=62°.