题目内容
5. 如图,AD与BC交于点E,∠BAC=∠ACD=90°,∠B=45°,∠D=30°,则$\frac{BE}{EC}$的值是$\frac{\sqrt{3}}{3}$.
如图,AD与BC交于点E,∠BAC=∠ACD=90°,∠B=45°,∠D=30°,则$\frac{BE}{EC}$的值是$\frac{\sqrt{3}}{3}$.
分析 解直角三角形得到AB=AC,CD=$\sqrt{3}$AC,通过AB∥CD,得到△ABE∽△CDE,根据相似三角形的性质即可得到结论.
解答 解:∵∠BAC=∠ACD=90°,∠B=45°,∠D=30°,
∴AB=AC,CD=$\sqrt{3}$AC,AB∥CD,
∴△ABE∽△CDE,
∴$\frac{BE}{EC}$=$\frac{AB}{CD}$=$\frac{AC}{\sqrt{3}AC}$=$\frac{\sqrt{3}}{3}$,
故答案为:$\frac{\sqrt{3}}{3}$.
点评 本题考查了相似三角形的判定和性质,解直角三角形,根据特殊角的三角函数得到AB=AC,CD=$\sqrt{3}$AC,是解题的关键.

练习册系列答案
相关题目
20.若2x3-ax2-5x+5=(2x2+ax-1)(x-b)+3,其中a,b为整数,则a+b的值为( )
| A. | -4 | B. | -2 | C. | 0 | D. | 4 |
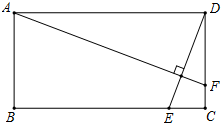 如图,矩形ABCD中,AB=2,AD=4,动点E在边BC上,与点B、C不重合,过点A作DE的垂线,交直线CD于点F,设DF=x,EC=y.
如图,矩形ABCD中,AB=2,AD=4,动点E在边BC上,与点B、C不重合,过点A作DE的垂线,交直线CD于点F,设DF=x,EC=y. 已知,如图所示,在?ABCD中,∠BAD的平分线与BC交于E,∠ABC的平分线交AD于点F,AE,BF交于O,则四边形ABEF为菱形,请说明理由.
已知,如图所示,在?ABCD中,∠BAD的平分线与BC交于E,∠ABC的平分线交AD于点F,AE,BF交于O,则四边形ABEF为菱形,请说明理由.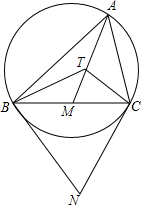 已知锐角△ABC及其外接圆,AM是边BC的中线,分别过点B,C作外接圆的切线,两条切线交于点N,T是AM上的一点,且∠ATC=∠ABN,求证:$\frac{AB}{AC}=\frac{TB}{TC}$.
已知锐角△ABC及其外接圆,AM是边BC的中线,分别过点B,C作外接圆的切线,两条切线交于点N,T是AM上的一点,且∠ATC=∠ABN,求证:$\frac{AB}{AC}=\frac{TB}{TC}$.
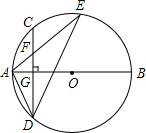 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3,给出下列结论:
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3,给出下列结论: