题目内容
2. 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
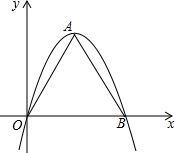
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.(1)如图,△OAB是抛物线y=-x2+bx(b>0)的“抛物线三角形”,当OA=OB时,求b的值;
(2)若抛物线y=a(x-2)2+b(a>0,b<0)的“抛物线三角形”是直角三角形,求a,b满足的关系.
分析 (1)由△OAB是抛物线y=-x2+bx(b>0)的“抛物线三角形”,当OA=OB时,易得△AOB是等边三角形,即可得点A的坐标为:($\frac{b}{2}$,$\frac{\sqrt{3}}{2}$b),继而求得答案;
(2)由于抛物线三角形是等腰三角形,则得到本题中的“物线三角形”是等腰直角三角形,再确定抛物线的顶点坐标为(2,b),即可求得抛物线与x轴两交点之间的线段长,然后根据等腰直角三角形的性质求解即可得到a与b的关系;
解答 解:(1)∵△OAB是抛物线y=-x2+bx(b>0)的“抛物线三角形”,
∴OA=AB,
∵OA=OB,
∴OA=OB=AB,
∴△AOB是等边三角形,
∵抛物线y=-x2+bx(b>0)与x轴交于点(0,0),(b,0),
∴OA=OB=b,
∴点A的坐标为:($\frac{b}{2}$,$\frac{\sqrt{3}}{2}$b),
∴抛物线解析式为:y=-(x-$\frac{b}{2}$)2+$\frac{\sqrt{3}}{2}$b,
∴-x2+bx=-(x-$\frac{b}{2}$)2+$\frac{\sqrt{3}}{2}$b,
∴$\frac{\sqrt{3}}{2}$b-$\frac{1}{4}$b2=0,
解得:b=2$\sqrt{3}$;
(2)∵y=a(x-2)2+b(ab<0)的“抛物线三角形”是直角三角形,
∴此“物线三角形”是等腰直角三角形,
抛物线的顶点坐标为(2,b),
把y=0代入y=a(x-2)2+b得a(x-2)2+b=0,解得x=2±$\sqrt{-\frac{b}{a}}$,
∴抛物线y=a(x-2)2+b(ab<0)与x轴两交点的坐标为(2+$\sqrt{-\frac{b}{a}}$,0),(2-$\sqrt{-\frac{b}{a}}$,0),
∴抛物线y=a(x-2)2+b(ab<0)与x轴两交点之间的线段长=2$\sqrt{-\frac{b}{a}}$,
∴|b|=$\frac{1}{2}$×2$\sqrt{-\frac{b}{a}}$,
∴b2=-$\frac{b}{a}$,
∴ab=-1.
点评 此题属于二次函数的综合题,考查了抛物线与x轴的交点问题、等边三角形的判定与性质以及等腰直角三角形性质.注意根据题意得到抛物线三角形分别是等边三角形与等腰直角三角形是解此题的关键.

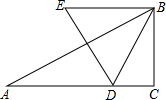 如图,已知△ABC,∠C=90°,∠A=30°,AC=$\sqrt{3}$,动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧),在点D从点A移动至点C的过程中,点E移动的路线为( )
如图,已知△ABC,∠C=90°,∠A=30°,AC=$\sqrt{3}$,动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧),在点D从点A移动至点C的过程中,点E移动的路线为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
| A. | (4,1) | B. | (5,1) | C. | (6,1) | D. | (7,1) |
 据国家教育部、卫生部最新调查表明:我国小学生近视率超过25%,初中生近视率达到70%,每年以8%的速度增长,居世界第一位.某市为调查中学生视力情况,从全市九年级学生中抽取了部分学生,统计了每个人连续三年视力检查的结果,并将所得数据处理后,制成统计表和扇形统计图如下:
据国家教育部、卫生部最新调查表明:我国小学生近视率超过25%,初中生近视率达到70%,每年以8%的速度增长,居世界第一位.某市为调查中学生视力情况,从全市九年级学生中抽取了部分学生,统计了每个人连续三年视力检查的结果,并将所得数据处理后,制成统计表和扇形统计图如下:被抽取学生视力在4.9以下的人数变化情况统计表
| 年份 | 2014 | 2015 | 2016 |
| 人数 | 300 | 500 | 800 |
(1)扇形统计图中x=10;
(2)该市共抽取了九年级学生2000名;
(3)若该市今年共有九年级学生约8.5万名,请你估计该市九年级学生视力不良(4.9以下)的学生大约有多少名?
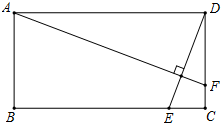 如图,矩形ABCD中,AB=2,AD=4,动点E在边BC上,与点B、C不重合,过点A作DE的垂线,交直线CD于点F,设DF=x,EC=y.
如图,矩形ABCD中,AB=2,AD=4,动点E在边BC上,与点B、C不重合,过点A作DE的垂线,交直线CD于点F,设DF=x,EC=y. 已知,如图所示,在?ABCD中,∠BAD的平分线与BC交于E,∠ABC的平分线交AD于点F,AE,BF交于O,则四边形ABEF为菱形,请说明理由.
已知,如图所示,在?ABCD中,∠BAD的平分线与BC交于E,∠ABC的平分线交AD于点F,AE,BF交于O,则四边形ABEF为菱形,请说明理由.