题目内容
18.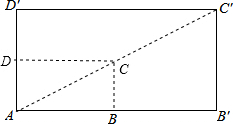 如图,矩形ABCD与矩形AB′C′D′是位似图形,已知矩形ABCD的周长是25cm,BB′=4cm,DD′=2cm,求矩形ABCD和AB′C′D′的面积比.
如图,矩形ABCD与矩形AB′C′D′是位似图形,已知矩形ABCD的周长是25cm,BB′=4cm,DD′=2cm,求矩形ABCD和AB′C′D′的面积比.
分析 设AB=x,然后利用x表示出AD,AD′,AB′的长,再由矩形ABCD与矩形A′B′C′D′是位似图形,根据位似图形的面积比等于相似比的平方可得方程,解方程得到答案.
解答 解:设AB=x,
∵矩形ABCD的周长为25,
∴AD=12.5-x,
∵BB′=4,DD′=2,
∴AD′=AD+DD′=14.5-x,AB′=AB+BB′=x+4,
∵矩形ABCD与矩形A′B′C′D′是位似图形,
∴$\frac{AB}{AB′}$=$\frac{AD}{AD′}$,即$\frac{x}{x+4}$=$\frac{12.5-x}{14.5-x}$,
解得,x=$\frac{25}{3}$,
则AB′=$\frac{37}{3}$,
矩形ABCD和AB′C′D′的面积比=($\frac{AB}{AB′}$)2=$\frac{625}{1369}$,
答:矩形ABCD和AB′C′D′的面积比为$\frac{625}{1369}$.
点评 本题考查的是位似变换,掌握位似图形的面积比等于相似比的平方是解题的关键.

练习册系列答案
相关题目
8.填表:
| 多边形的边数 | 7 | 17 | 20 | 25 |
| 内角和 | 5×180° | 15×180° | 18×180° | 23×180° |
| 外角和 | 360° | 360° | 360° | 360° |
6.已知直角三角形的两边长是3和5,则此三角形的第三边长是( )
| A. | 4 | B. | $\sqrt{34}$ | C. | 4或$\sqrt{34}$ | D. | 以上都不对 |

 如图,AB∥CD,AD与BC交于O点,AO=4,OB=6,AD=16,求BC、OC.
如图,AB∥CD,AD与BC交于O点,AO=4,OB=6,AD=16,求BC、OC.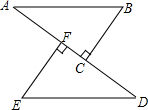 如图,AB=DE,BC⊥AD,EF⊥AD,垂足分别为C、F,且AF=DC,求证:AB∥DE.
如图,AB=DE,BC⊥AD,EF⊥AD,垂足分别为C、F,且AF=DC,求证:AB∥DE.