题目内容
4. 如图,AB∥CD,BF与CD相交于点E,联结DF,那么∠B和∠F、∠D的数量关系是∠B=∠F+∠D.
如图,AB∥CD,BF与CD相交于点E,联结DF,那么∠B和∠F、∠D的数量关系是∠B=∠F+∠D.
分析 根据平行线的性质得出∠B=∠BED,根据三角形的外角性质得出∠BED=∠F+∠D,即可得出答案.
解答 解:∠B=∠F+∠D,
理由是:∵AB∥CD,
∴∠B=∠BED,
∵∠BED=∠F+∠D,
∴∠B=∠F+∠D,
故答案为:∠B=∠F+∠D.
点评 本题考查了平行线的性质和三角形外角性质的应用,能根据平行线的性质得出∠B=∠BED是解此题的关键.

练习册系列答案
相关题目
14.菱形具有而矩形不一定具有的性质是( )
| A. | 对角相等 | B. | 每条对角线平分一组对角 | ||
| C. | 对角线互相平分 | D. | 对边平行且相等 |
13.等腰三角形的两边分别是3和6,则周长是( )
| A. | 9 | B. | 12 | C. | 15 | D. | 12或15 |
 如图所示,⊙O是△ABC 的外接圆,AB是直径,∠ABC=30°,点E是OC的中点,连接AE并延长交⊙○于点D,连接OD,CD,BD.
如图所示,⊙O是△ABC 的外接圆,AB是直径,∠ABC=30°,点E是OC的中点,连接AE并延长交⊙○于点D,连接OD,CD,BD.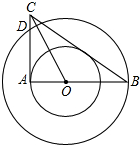 如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A,与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A,与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB. 在?ABCD中,∠A比∠B大30°,求∠C的度数.
在?ABCD中,∠A比∠B大30°,求∠C的度数. 如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O,求证:△ABC≌△DCB.
如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O,求证:△ABC≌△DCB.