题目内容
5. 如图,△ABC为等边三角形,BD平分∠ABC,DE∥BC.
如图,△ABC为等边三角形,BD平分∠ABC,DE∥BC.(1)说明△BDE是等腰三角形;
(2)△ADE是什么三角形?AE与AB的大小有什么关系?为什么?
分析 (1)根据△ABC为等边三角形,得到∠ABC=60°,根据BD平分∠ABC,得到∠ABD=∠CBD=30°,根据DE∥BC得到∠EDB=∠DBC,证明结论;
(2)根据等边三角形的判定和平行线的性质证明即可.
解答 证明:(1)∵△ABC为等边三角形,
∴∠ABC=60°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=30°,
∵DE∥BC,
∴∠EDB=∠DBC,
∴∠EDB=∠DBE,
∴△BDE是等腰三角形;
(2)∵DE∥BC,
∴∠AED=∠ABC=60°,∠ADE=∠ACB=60°,
∴△ADE是等边三角形,
∵BD平分∠ABC,
∴D是AC的中点,又DE∥BC,
∴E是AB的中点,
∴AE=$\frac{1}{2}$AB.
点评 本题考查的是等边三角形的判定和性质、等腰三角形的判定,掌握判定定理并灵活运用定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.下列几种形状的瓷砖中,只用一种不能够铺满地面的是( )
| A. | 正三角形 | B. | 正四边形 | C. | 正五边形 | D. | 正六边形 |
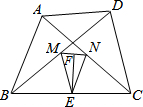 如图所示,在四边形ABCD中,AB=CD,点M,N,E,F分别是BD,AC,BC,MN的中点,连接ME,NE.
如图所示,在四边形ABCD中,AB=CD,点M,N,E,F分别是BD,AC,BC,MN的中点,连接ME,NE.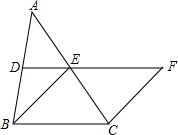 如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF
如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF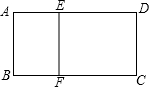 如图,矩形ABCD中,AB=2cm,AD=4cm,点E,F分别在AD,BC边上,AE=BF=1cm,求证:矩形ABFE∽矩形ADCB.
如图,矩形ABCD中,AB=2cm,AD=4cm,点E,F分别在AD,BC边上,AE=BF=1cm,求证:矩形ABFE∽矩形ADCB.

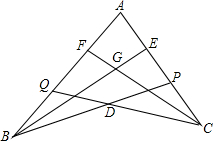 如图,点P在AC上,点Q在AB上,BE平分∠ABP,交AC于E,CF平分∠ACQ,交AB于F,BE、CF相交于G,CQ、BP相交于D,若∠BDC=140°,∠BGC=110°,求∠A的度数.
如图,点P在AC上,点Q在AB上,BE平分∠ABP,交AC于E,CF平分∠ACQ,交AB于F,BE、CF相交于G,CQ、BP相交于D,若∠BDC=140°,∠BGC=110°,求∠A的度数.