题目内容
7.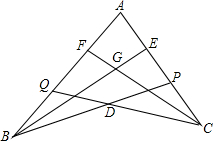 如图,点P在AC上,点Q在AB上,BE平分∠ABP,交AC于E,CF平分∠ACQ,交AB于F,BE、CF相交于G,CQ、BP相交于D,若∠BDC=140°,∠BGC=110°,求∠A的度数.
如图,点P在AC上,点Q在AB上,BE平分∠ABP,交AC于E,CF平分∠ACQ,交AB于F,BE、CF相交于G,CQ、BP相交于D,若∠BDC=140°,∠BGC=110°,求∠A的度数.
分析 根据三角形的内角和定理,及角平分线上的性质先计算∠ABC+∠ACB的度数,从而得出∠A的度数.
解答 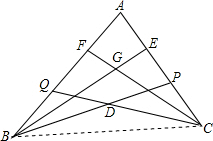 解:如图,连接BC.
解:如图,连接BC.
∵BE是∠ABD的平分线,CF是∠ACD的平分线,
∴∠ABE=∠DBE=$\frac{1}{2}$∠ABD,∠ACF=∠DCF=$\frac{1}{2}$∠ACD,
又∠BDC=140°,∠BGC=110°,
∴∠DBC+∠DCB=40°,∠GBC+∠GCB=70°,
∴∠EBD+∠FCD=70°-40°=30°,
∴∠ABE+∠ACF=30°,
∴∠ABE+∠ACF+∠GBC+∠GCB=70°+30°=100°,即∠ABC+∠ACB=100°,
∴∠A=80°.
点评 本题考查角平分线的性质及三角形的内角和定理,根据题意作出辅助线,构造出三角形是解答此题的关键.

练习册系列答案
相关题目
2.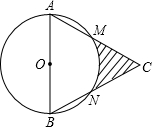 如图,等边△ABC边长为12cm,以AB为直径的⊙O分别交CA、CB于M、N两点,则图中阴影部分的面积是( )
如图,等边△ABC边长为12cm,以AB为直径的⊙O分别交CA、CB于M、N两点,则图中阴影部分的面积是( )
 如图,等边△ABC边长为12cm,以AB为直径的⊙O分别交CA、CB于M、N两点,则图中阴影部分的面积是( )
如图,等边△ABC边长为12cm,以AB为直径的⊙O分别交CA、CB于M、N两点,则图中阴影部分的面积是( )| A. | 9$\sqrt{3}$-6π | B. | 18$\sqrt{3}$-6π | C. | 12$\sqrt{3}$-3π | D. | 12$\sqrt{3}$-6π |
 如图,△ABC为等边三角形,BD平分∠ABC,DE∥BC.
如图,△ABC为等边三角形,BD平分∠ABC,DE∥BC. 如图,在矩形ABCD中,AB=8,AD=12,过A,D两点的⊙O与BC边相切于点E,则⊙O的半径为6.25.
如图,在矩形ABCD中,AB=8,AD=12,过A,D两点的⊙O与BC边相切于点E,则⊙O的半径为6.25.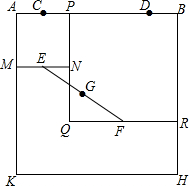 如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为( )
如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为( )