题目内容
14.小明随机调查了若干市民租用公共自行车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如图统计图,请根据图中信息,解答下列问题:
(1)这次被调查的总人数是多少?
(2)试求表示A组的扇形圆心角的度数,并补全条形统计图.
(3)如果骑自行车的平均速度为12km/h,请估算,在租用公共自行车的市民中,骑车路程不超过6km的人数所占的百分比.
分析 (1)根据B类人数是19,所占的百分比是38%,据此即可求得调查的总人数;
(2)利用360°乘以对应的百分比即可求解;
(3)求得路程是6km时所用的时间,根据百分比的意义可求得路程不超过6km的人数所占的百分比.
解答 解:(1)调查的总人数是:19÷38%=50(人);
(2)A组所占圆心角的度数是:360×$\frac{15}{50}$=108°,
C组的人数是:50-15-19-4=12. ;
;
(3)路程是6km时所用的时间是:6÷12=0.5(小时)=30(分钟),
则骑车路程不超过6km的人数所占的百分比是:$\frac{50-4}{50}$×100%=92%.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列运算正确的是( )
| A. | $\sqrt{(-11)^{2}}$=-11 | B. | 2$\sqrt{2}$-$\sqrt{2}$=1 | ||
| C. | (-$\sqrt{2}$)2=2 | D. | $\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{{3}^{2}}$+$\sqrt{{2}^{2}}$=3+2=5 |
2. 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )| A. | 35° | B. | 40° | C. | 50° | D. | 65° |
 如图,△ABC为等边三角形,BD平分∠ABC,DE∥BC.
如图,△ABC为等边三角形,BD平分∠ABC,DE∥BC.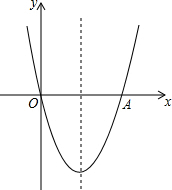 如图,抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.
如图,抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.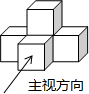 如图是由五个相同的小立方块搭成的几何体,则它的俯视图是( )
如图是由五个相同的小立方块搭成的几何体,则它的俯视图是( )
 如图,在矩形ABCD中,AB=8,AD=12,过A,D两点的⊙O与BC边相切于点E,则⊙O的半径为6.25.
如图,在矩形ABCD中,AB=8,AD=12,过A,D两点的⊙O与BC边相切于点E,则⊙O的半径为6.25.