题目内容
13.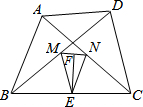 如图所示,在四边形ABCD中,AB=CD,点M,N,E,F分别是BD,AC,BC,MN的中点,连接ME,NE.
如图所示,在四边形ABCD中,AB=CD,点M,N,E,F分别是BD,AC,BC,MN的中点,连接ME,NE.(1)试猜想△MEN的形状,并证明你的猜想正确;
(2)EF与MN有何位置关系?请证明你的结论.
分析 (1)利用三角形中位线定理得到ME=$\frac{1}{2}$CD,NE=$\frac{1}{2}$AB,结合“AB=CD”推知△MEN是等腰三角形;
(2)根据等腰三角形“三线合一”的性质证得EF⊥MN.
解答 解:(1)△MEN是等腰三角形.理由如下:
∵点M是BD的中点,
∴ME是△BCD的中位线,
∴ME=$\frac{1}{2}$CD.
同理,NE=$\frac{1}{2}$AB.
又∵AB=CD,
∴ME=NE,
∴△MEN是等腰三角形;
(2)EF⊥MN.理由如下:
由(1)知,△MEN是等腰三角形.
∵F是MN的中点,
∴EF⊥MN.
点评 本题考查了三角形中位线定理和等腰三角形的判定与性质.等腰三角形提供了好多相等的线段和相等的角,判定三角形是等腰三角形是证明线段相等、角相等的重要手段.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
3.在一次“探究性学习”课中,老师设计如下数表:
(1)观察表格,根据规律在表中填空.
(2)用含自然数n(n>1)的代数式表示a、b、c,则a=n2-1,b=2n,c=n2+1.
(3)猜想:以a,b,c为边的三角形是否为直角三角形?证明你的结论.
| n | 2 | 3 | 4 | 5 | 6 | … |
| a | 22-1 | 32-1 | 42-1 | 52-1 | 62-1 | … |
| b | 4 | 6 | 8 | 10 | 12 | … |
| c | 22+1 | 32+1 | 42+1 | 52+1 | 62+1 | … |
(2)用含自然数n(n>1)的代数式表示a、b、c,则a=n2-1,b=2n,c=n2+1.
(3)猜想:以a,b,c为边的三角形是否为直角三角形?证明你的结论.
4.下列运算正确的是( )
| A. | $\sqrt{(-11)^{2}}$=-11 | B. | 2$\sqrt{2}$-$\sqrt{2}$=1 | ||
| C. | (-$\sqrt{2}$)2=2 | D. | $\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{{3}^{2}}$+$\sqrt{{2}^{2}}$=3+2=5 |
2. 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )| A. | 35° | B. | 40° | C. | 50° | D. | 65° |
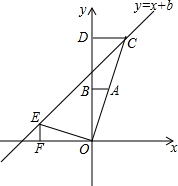 如图,在平面直角坐标系中,点O是坐标原点,Rt△OAB的直角顶点B在y轴的正半轴上,以原点O为位似中心,位似比为2:1,把△OAB放大,放大后的三角形为△OCD,把△OAB绕点O逆时针旋转90°后得△OEF,点A的坐标是(1,t).
如图,在平面直角坐标系中,点O是坐标原点,Rt△OAB的直角顶点B在y轴的正半轴上,以原点O为位似中心,位似比为2:1,把△OAB放大,放大后的三角形为△OCD,把△OAB绕点O逆时针旋转90°后得△OEF,点A的坐标是(1,t).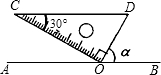 如图,一块含有60°三角板的顶点O在直线AB上,CD∥AB.则∠α=60度.
如图,一块含有60°三角板的顶点O在直线AB上,CD∥AB.则∠α=60度.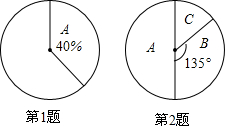 根据扇形统计图,解决下列问题:
根据扇形统计图,解决下列问题: 如图,△ABC为等边三角形,BD平分∠ABC,DE∥BC.
如图,△ABC为等边三角形,BD平分∠ABC,DE∥BC.