题目内容
15．如果点P（2，-4），Q（x，-4）之间的距离是3，那么x的值为-1或5．分析 根据P点和Q点的坐标特征得到PQ∥x轴，则|2-x|=3，然后解绝对值方程即可．
解答 解：根据题意得|2-x|=3，
解得x=-1或5．
故答案为-1或5．
点评 本题考查了坐标与图形性质：利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系；记住两点间的距离公式．
练习册系列答案
相关题目
5．
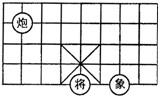如图，象棋盘上“将”位于点（1，-2），则“炮”位于点（ ）
如图，象棋盘上“将”位于点（1，-2），则“炮”位于点（ ）| A． | （-3，3） | B． | （3，3） | C． | （-2，1） | D． | （-2，3） |
3．在一次“探究性学习”课中，老师设计如下数表：
（1）观察表格，根据规律在表中填空．
（2）用含自然数n（n＞1）的代数式表示a、b、c，则a=n2-1，b=2n，c=n2+1．
（3）猜想：以a，b，c为边的三角形是否为直角三角形？证明你的结论．
| n | 2 | 3 | 4 | 5 | 6 | … |
| a | 22-1 | 32-1 | 42-1 | 52-1 | 62-1 | … |
| b | 4 | 6 | 8 | 10 | 12 | … |
| c | 22+1 | 32+1 | 42+1 | 52+1 | 62+1 | … |
（2）用含自然数n（n＞1）的代数式表示a、b、c，则a=n2-1，b=2n，c=n2+1．
（3）猜想：以a，b，c为边的三角形是否为直角三角形？证明你的结论．
10．
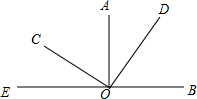如图，已知AO⊥BE于O点，CO⊥DO于O点，∠BOC=α，则∠AOD的度数为（ ）
如图，已知AO⊥BE于O点，CO⊥DO于O点，∠BOC=α，则∠AOD的度数为（ ）| A． | α-90° | B． | 2α-90° | C． | 180°-α | D． | 2α-180° |
7．在△ABC中，∠ABC=30°，∠BAC=70°．在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画（ ）
| A． | 7条 | B． | 8条 | C． | 9条 | D． | 10条 |
4．下列运算正确的是（ ）
| A． | $\sqrt{（-11）^{2}}$=-11 | B． | 2$\sqrt{2}$-$\sqrt{2}$=1 | ||
| C． | （-$\sqrt{2}$）2=2 | D． | $\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{{3}^{2}}$+$\sqrt{{2}^{2}}$=3+2=5 |
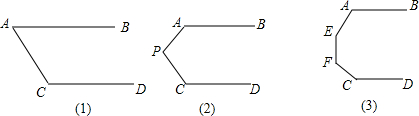
如图，△ABC为等边三角形，BD平分∠ABC，DE∥BC．