题目内容
10.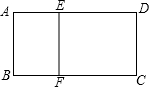 如图,矩形ABCD中,AB=2cm,AD=4cm,点E,F分别在AD,BC边上,AE=BF=1cm,求证:矩形ABFE∽矩形ADCB.
如图,矩形ABCD中,AB=2cm,AD=4cm,点E,F分别在AD,BC边上,AE=BF=1cm,求证:矩形ABFE∽矩形ADCB.
分析 根据矩形的性质得出∠A=∠B=∠C=∠D=90°,AB=CD=2cm,AD=BC=4cm,AD∥BC,求出四边形AEFB是矩形,推出∠AEF=∠EFB=90°,AB=EF=2cm,求出∠A=∠A,∠AEF=∠B,∠B=∠D,∠EFB=∠C,$\frac{AE}{AB}$=$\frac{BF}{CD}$=$\frac{AB}{AD}$=$\frac{EF}{BC}$=$\frac{1}{2}$,根据多边形相似的判定定理推出即可.
解答 证明:∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°,AB=CD=2cm,AD=BC=4cm,AD∥BC,
即AE∥BF,
∵AE=BF,
∴四边形AEFB是矩形,
∴∠AEF=∠EFB=90°,AB=EF=2cm,
∴∠A=∠A,∠AEF=∠B,∠B=∠D,∠EFB=∠C,$\frac{AE}{AB}$=$\frac{BF}{CD}$=$\frac{AB}{AD}$=$\frac{EF}{BC}$=$\frac{1}{2}$,
∴矩形ABFE∽矩形ADCB.
点评 本题考查了矩形的性质和判定,相似多边形的判定定理的应用,能求出∠A=∠A、∠AEF=∠B、∠B=∠D、∠EFB=∠C、$\frac{AE}{AB}$=$\frac{BF}{CD}$=$\frac{AB}{AD}$=$\frac{EF}{BC}$=$\frac{1}{2}$是解此题的关键,难度适中.

练习册系列答案
相关题目
2. 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )| A. | 35° | B. | 40° | C. | 50° | D. | 65° |
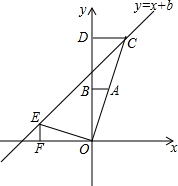 如图,在平面直角坐标系中,点O是坐标原点,Rt△OAB的直角顶点B在y轴的正半轴上,以原点O为位似中心,位似比为2:1,把△OAB放大,放大后的三角形为△OCD,把△OAB绕点O逆时针旋转90°后得△OEF,点A的坐标是(1,t).
如图,在平面直角坐标系中,点O是坐标原点,Rt△OAB的直角顶点B在y轴的正半轴上,以原点O为位似中心,位似比为2:1,把△OAB放大,放大后的三角形为△OCD,把△OAB绕点O逆时针旋转90°后得△OEF,点A的坐标是(1,t).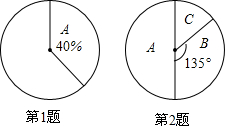 根据扇形统计图,解决下列问题:
根据扇形统计图,解决下列问题: 如图,△ABC为等边三角形,BD平分∠ABC,DE∥BC.
如图,△ABC为等边三角形,BD平分∠ABC,DE∥BC.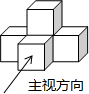 如图是由五个相同的小立方块搭成的几何体,则它的俯视图是( )
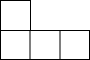
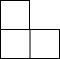
如图是由五个相同的小立方块搭成的几何体,则它的俯视图是( )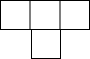
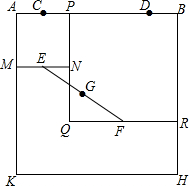 如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为( )
如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为( )