题目内容
16．下列几种形状的瓷砖中，只用一种不能够铺满地面的是（ ）| A． | 正三角形 | B． | 正四边形 | C． | 正五边形 | D． | 正六边形 |
分析 根据平面图形镶嵌的条件：判断一种图形是否能够镶嵌，只要看一看拼在同一顶点处的几个角能否构成周角．若能构成360°，则说明能够进行平面镶嵌；反之则不能，对于一种正多边形的镶嵌应符合一个内角度数能整除360°，依此即可得出答案．
解答 解：A、正三角形的每个内角是60°，能整除360°，能密铺；
B、正四边形的每个内角是90°，能整除360°，能密铺；
C、正五边形每个内角是180°-360°÷5=108°，不能整除360°，不能密铺；
D、正六边形的每个内角是120°，能整除360°，能密铺．
故选C．
点评 此题考查了平面镶嵌，用到的知识点是只用一种正多边形能够铺满地面的是正三角形或正四边形或正六边形．
练习册系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
7．在△ABC中，∠ABC=30°，∠BAC=70°．在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画（ ）
| A． | 7条 | B． | 8条 | C． | 9条 | D． | 10条 |
4．下列运算正确的是（ ）
| A． | $\sqrt{（-11）^{2}}$=-11 | B． | 2$\sqrt{2}$-$\sqrt{2}$=1 | ||
| C． | （-$\sqrt{2}$）2=2 | D． | $\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{{3}^{2}}$+$\sqrt{{2}^{2}}$=3+2=5 |
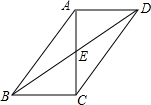如图，在?ABCD中，对角线AC，BD交于点E，AC⊥BC，若BC=5，AB=13，则BD的长是2$\sqrt{61}$．
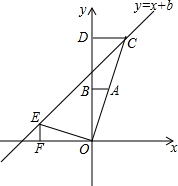如图，在平面直角坐标系中，点O是坐标原点，Rt△OAB的直角顶点B在y轴的正半轴上，以原点O为位似中心，位似比为2：1，把△OAB放大，放大后的三角形为△OCD，把△OAB绕点O逆时针旋转90°后得△OEF，点A的坐标是（1，t）．
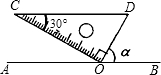如图，一块含有60°三角板的顶点O在直线AB上，CD∥AB．则∠α=60度．
如图，△ABC为等边三角形，BD平分∠ABC，DE∥BC．
如图，在矩形ABCD中，AB=8，AD=12，过A，D两点的⊙O与BC边相切于点E，则⊙O的半径为6.25．