题目内容
15. 如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从点A出发,以每秒1cm的速度沿AC运动;同时点Q从点C出发,以每秒2cm的速度沿CB运动,当Q到达点B时,点P同时停止运动.
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从点A出发,以每秒1cm的速度沿AC运动;同时点Q从点C出发,以每秒2cm的速度沿CB运动,当Q到达点B时,点P同时停止运动.(1)求运动几秒时△PCQ的面积为5cm2?
(2)△PCQ的面积能否等于10cm2?若能,求出运动时间,若不能,说明理由.
分析 (1)设运动t秒后△PCQ的面积等于5cm,分别表示出线段CP和线段CQ的长,再利用三角形的面积公式列出方程求解即可.
(2)根据配方法可求△PCQ的面积能否等于10cm2.
解答 解:设运动t秒后△PCQ的面积等于5cm,根据题意得:
CP=6-t,QC=2t,
则△PCQ的面积是:
$\frac{1}{2}$CQ•CP=$\frac{1}{2}$×(6-t)×2t=5,
解得t1=1,t2=5(舍去),
故经过1秒后,△PCQ的面积等于5cm2.
(2)$\frac{1}{2}$×(6-t)×2t=-t2+6t=-(t-3)2+9,
故△PCQ的面积最大为9,不能等于10cm2.
点评 本题考查了一元二次方程的应用,解题的关键是根据题意找到等量关系并列出方程,用到的知识点是三角形的面积公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DE保持水平,并且边DE与点B在同一条直线上.已知纸板的两条边DE=70cm,EF=30cm,测得AC=$\frac{7}{8}$m,BD=9m,求树高AB.
如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DE保持水平,并且边DE与点B在同一条直线上.已知纸板的两条边DE=70cm,EF=30cm,测得AC=$\frac{7}{8}$m,BD=9m,求树高AB. 如图:甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形.两圆心中心各有一个可以自由转动的指针,随机地转动指针(当指针指在边界线上时视为无效,重转).请回答下列问题.
如图:甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形.两圆心中心各有一个可以自由转动的指针,随机地转动指针(当指针指在边界线上时视为无效,重转).请回答下列问题.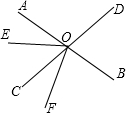 如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.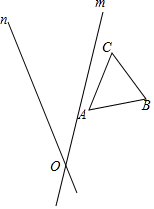 如图,直线m,n的夹角为35°,相交于点O,
如图,直线m,n的夹角为35°,相交于点O,