题目内容
8.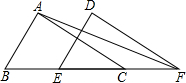 如图,已知△ABC的面积为16,BC=8,∠ACB=42°,现将△ABC沿直线BC向右平移a个单位到△DEF
如图,已知△ABC的面积为16,BC=8,∠ACB=42°,现将△ABC沿直线BC向右平移a个单位到△DEF(1)连接AF,若AF平分∠DFE,求∠FAC的大小.
(2)当△ABC所扫过的面积为32时,求a的值.
分析 (1)根据平行的性质AC∥DF且∠ACB=∠DFE,然后根据角的平分线的定义以及平行线的性质即可求解;
(2)△ABC扫过的面积等于△ABC的面积加上平行四边形ABED的面积,根据平行四边形的面积公式即可求解.
解答 解:(1)∵FA平分∠DFE,
∴∠DFA=$\frac{1}{2}$∠DFE=$\frac{1}{2}$∠ACB=$\frac{1}{2}$×42°=21°,
∵AC∥DF,
∴∠FAC=∠DFA=21°;
(2)BC边上的高是2×$\frac{16}{8}$=4,
根据题意得:4a+16=32,
解得:a=4.
点评 本题考查了图形的平移,正确理解△ABC扫过的面积等于△ABC的面积加上平行四边形ABED的面积是关键.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
19.一个正方形的面积为21,它的边长为a,则a-1的边长大小为( )
| A. | 2与3之间 | B. | 3与4之间 | C. | 4与5之间 | D. | 5与6之间 |
3.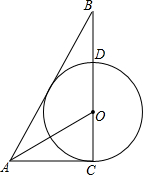 如图,在Rt△ABC中,△ACB=90°,点0在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D,若BD=1,tan∠AOC=2,则⊙O的面积是( )
如图,在Rt△ABC中,△ACB=90°,点0在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D,若BD=1,tan∠AOC=2,则⊙O的面积是( )
 如图,在Rt△ABC中,△ACB=90°,点0在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D,若BD=1,tan∠AOC=2,则⊙O的面积是( )
如图,在Rt△ABC中,△ACB=90°,点0在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D,若BD=1,tan∠AOC=2,则⊙O的面积是( )| A. | π | B. | 2π | C. | $\frac{9}{4}$π | D. | $\frac{16}{9}$π |
17.在同一平面内,直线AB与CD相交于点O,如果AB∥EF,那么CD与EF的位置关系是( )
| A. | 平行 | B. | 相交 | C. | 平行或相交 | D. | 无法确定 |
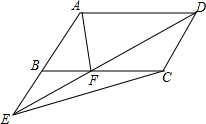 如图所示,E是?ABCD的边AB延长线上一点,DE交BC于F,求证:S△ABF=S△EFC.
如图所示,E是?ABCD的边AB延长线上一点,DE交BC于F,求证:S△ABF=S△EFC.