题目内容
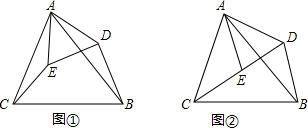
16.如图①,在有公共顶点的△ABC和△ADE中,AB=AC,AD=AE,且∠CAB=∠EAD.(1)求证:CE=BD;
(2)若将△ADE绕点A沿逆时针方向旋转使点C、E、D在同一条直线上时,如图②,(1)中的结论是否仍然成立?如果结论成立,请证明;如果结论不成立,请说明理由.
分析 (1)根据∠CAB=∠EAD求出∠CAE=∠BAD,根据SAS推出△CAE≌△BAD,根据全等三角形的性质得出即可;
(2)根据∠CAB=∠EAD求出∠CAE=∠BAD,根据SAS推出△CAE≌△BAD,根据全等三角形的性质得出即可.
解答 (1)证明:∵∠CAB=∠EAD,
∴∠CAB-∠EAB=∠EAD-∠EAB,
∴∠CAE=∠BAD,
在△CAE和△BAD中
$\left\{\begin{array}{l}{AC=AB}\\{∠CAE=∠BAD}\\{AE=AD}\end{array}\right.$
∴△CAE≌△BAD(SAS),
∴CE=BD;
(2)结论还成立,
证明:∵∠CAB=∠EAD,
∴∠CAB-∠EAB=∠EAD-∠EAB,
∴∠CAE=∠BAD,
在△CAE和△BAD中
$\left\{\begin{array}{l}{AC=AB}\\{∠CAE=∠BAD}\\{AE=AD}\end{array}\right.$
∴△CAE≌△BAD(SAS),
∴CE=BD.
点评 本题考查了全等三角形的性质和判定的应用,能求出△CAE≌△BAD是解此题的关键,注意:全等三角形的对应边相等.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
7.已知x+y=6,xy=4,则x2y+xy2的值为( )
| A. | 12 | B. | -12 | C. | -24 | D. | 24 |
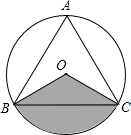 如图,等边△ABC内接于⊙O,AB=4$\sqrt{3}$.
如图,等边△ABC内接于⊙O,AB=4$\sqrt{3}$.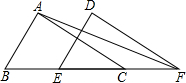 如图,已知△ABC的面积为16,BC=8,∠ACB=42°,现将△ABC沿直线BC向右平移a个单位到△DEF
如图,已知△ABC的面积为16,BC=8,∠ACB=42°,现将△ABC沿直线BC向右平移a个单位到△DEF 已知,如图AB=CB,AD=CD,∠A=110°,求∠C的度数.
已知,如图AB=CB,AD=CD,∠A=110°,求∠C的度数.