题目内容
13．已知P=m2-$\frac{2}{3}$m，Q=$\frac{4}{3}$m-2（m为任意实数）（1）请判断P，Q的大小关系，并说明理由；
（2）当m=1时，P-Q有最小值，为1．
分析 （1）先求出P-Q的差，再利用完全平方公式配方，根据偶次方的性质即可即可得出P，Q的大小关系；
（2）根据非负数的性质即可求解．
解答 解：（1）P＞Q，理由如下：
∵P=m2-$\frac{2}{3}$m，Q=$\frac{4}{3}$m-2（m为任意实数），
∴P-Q=（m2-$\frac{2}{3}$m）-（$\frac{4}{3}$m-2）=m2-2m+2=（m-1）2+1＞0，
∴P＞Q；
（2）∵P-Q=（m-1）2+1，
而（m-1）2≥0，
∴当m=1时，（m-1）2有最小值，此时P-Q有最小值1．
故答案为：1，1．
点评 此题考查配方法的应用和偶次方的性质，掌握比较大小的常用方法是关键．
练习册系列答案
相关题目
3．
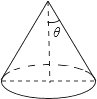已知圆锥的底面半径为3cm，侧面积为15πcm2，设圆锥的母线与高的夹角为θ（如图所示），则tanθ的值为（ ）
已知圆锥的底面半径为3cm，侧面积为15πcm2，设圆锥的母线与高的夹角为θ（如图所示），则tanθ的值为（ ）| A． | $\frac{3}{5}$ | B． | $\frac{3}{4}$ | C． | $\frac{4}{3}$ | D． | $\frac{4}{5}$ |
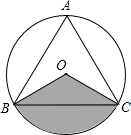如图，等边△ABC内接于⊙O，AB=4$\sqrt{3}$．
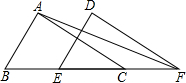如图，已知△ABC的面积为16，BC=8，∠ACB=42°，现将△ABC沿直线BC向右平移a个单位到△DEF