已知a2+a-1=0.则2a3+4a2+2015的值是2017．题目和参考答案——青夏教育精英家教网—

题目内容

17．已知a²+a-1=0，则2a³+4a²+2015的值是2017．

分析先将已知条件变形为a²=1-a、a²+a=1，然后逐步代入代数式2a³+4a²+2015中，再进行计算即可得出答案

解答解：∵a²+a-1=0，
∴a²=1-a、a²+a=1，
∴2a³+4a²+2015
=2a•a²+4（1-a）+2015
=2a（1-a）+4-4a+2015
=2a-2a²-4a+2019
=-2a²-2a+2019
=-2（a²+a）+2019
=-2+2019
=2017．
故答案为：2017．

点评此题考查了因式分解的应用，解题的关键是根据因式分解对整式部分变形，把复杂问题转化为简单问题，渗透了整体思想．

练习册系列答案

相关题目

7．已知x+y=6，xy=4，则x²y+xy²的值为（　　）

8．

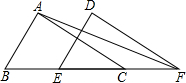如图，已知△ABC的面积为16，BC=8，∠ACB=42°，现将△ABC沿直线BC向右平移a个单位到△DEF
（1）连接AF，若AF平分∠DFE，求∠FAC的大小．
（2）当△ABC所扫过的面积为32时，求a的值．

5．已知一次函数y=-2x+6的图象与x轴、y轴分别相交于A、B两点，点C坐标（2，0），点D在直线y=-2x+6上，△OCD的面积是△AOB的面积的$\frac{1}{4}$，则点D的坐标为（$\frac{15}{8}$，-$\frac{9}{4}$）或（$\frac{33}{8}$，-$\frac{9}{4}$）．

12．$\frac{1}{2}$x^m+n-5-$\frac{1}{3}$y^2m-4n+1=0是二元一次方程，求m和n的值．

1．如图①，在矩形ABCD中，AD=6，∠BDC=30°，将△BCD绕点B逆作时针方向旋转得到△BC₀D₀，其中点C，D的对应点分别是点C₀，D₀，且点D₀刚好落在CB的延长线上，直线D₀C₀与AB相交于点E；

（1）求旋转角α的度数；
（2）求△EBD₀的面积；
（3）如图②，将△BC₀D₀以每秒1个单位长度的速度向右平行移动，得到△B₁C₁D₁，其中点B，C₀，D₀的对应点分别是点B₁C₁D₁，当点C₁到达边CD上时停止运动，设移动的时间为t秒，△B₁C₁D₁与矩形ABCD重叠部分的面积为S（图中阴影部分），请直接写出S关于t的函数关系式，并写出t的取值范围；
（4）如题③，在（3）的△B₁C₁D₁平移过程中，直线D₁C₁与线段AB相交于N，直线B₁C₁与线段BD相交于M，是否存在某一时刻t，使△MNC为等腰三角形，若存在，求出时间t，若不存在，请说明理由．

8．

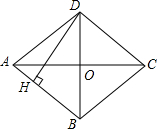如图，四边形ABCD是菱形，对角线AC=8cm，BD=6 cm，DH⊥AB于H，DH的长是$\frac{24}{5}$cm．

5．

已知，如图AB=CB，AD=CD，∠A=110°，求∠C的度数．

6．如果一个三角形的一条边是另一条边的2倍，并且有一个角是30°，那么这个三角形的形状是（　　）

试题分类