题目内容
20.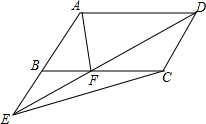 如图所示,E是?ABCD的边AB延长线上一点,DE交BC于F,求证:S△ABF=S△EFC.
如图所示,E是?ABCD的边AB延长线上一点,DE交BC于F,求证:S△ABF=S△EFC.
分析 分别过点E、D作EG⊥BC、DH⊥BC,交直线BC于G、H,根据平行四边形的性质得出BE∥CD,那么△BEF∽△CDF,利用相似三角形对应高的比等于相似比得到BF•DH=CF•EG,即可解决问题.
解答  解:如图,分别过点E、D作EG⊥BC、DH⊥BC,交直线BC于G、H.
解:如图,分别过点E、D作EG⊥BC、DH⊥BC,交直线BC于G、H.
∵四边形ABCD是平行四边形,
∴BE∥CD,
∴△BEF∽△CDF,
∴$\frac{BF}{CF}$=$\frac{EG}{DH}$,即BF•DH=CF•EG,
∵S△ABF=$\frac{1}{2}$BF•DH,S△EFC=$\frac{1}{2}$CF•EG,
∴S△ABF=S△EFC.
点评 该题主要考查了平行四边形的性质、相似三角形的判定及性质,三角形的面积等知识;解题的关键是正确作出辅助线.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.一个多边形的内角和是外角和的n倍(n是正整数),则该多边形的边数是( )
| A. | 2n+2 | B. | n+1 | C. | 2n+1 | D. | 2n+4 |
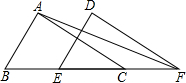 如图,已知△ABC的面积为16,BC=8,∠ACB=42°,现将△ABC沿直线BC向右平移a个单位到△DEF
如图,已知△ABC的面积为16,BC=8,∠ACB=42°,现将△ABC沿直线BC向右平移a个单位到△DEF 如图,在?ABCD中,AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长为4cm.
如图,在?ABCD中,AD=12cm,AB=8cm,AE平分∠BAD交BC边于点E,则CE的长为4cm.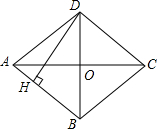 如图,四边形ABCD是菱形,对角线AC=8cm,BD=6 cm,DH⊥AB于H,DH的长是$\frac{24}{5}$cm.
如图,四边形ABCD是菱形,对角线AC=8cm,BD=6 cm,DH⊥AB于H,DH的长是$\frac{24}{5}$cm.