题目内容
18．分解因式（1）8（x2-2y2）-x（7x+y）+xy．
（2）a2-b2+ac+bc．
分析 （1）首先去括号，进而合并同类项，再利用平方差公式分解因式即可；
（2）将前两项和后两项分别组合进而提取公因式分解因式即可．
解答 解：（1）8（x2-2y2）-x（7x+y）+xy
=8x2-16y2-7x2-xy+xy
=x2-16y2
=（x+4y）（x-4y）；
（2）a2-b2+ac+bc
=（a+b）（a-b）+c（a+b）
=（a+b）（a-b+c）．
点评 此题主要考查了公式法分解因式，熟练应用乘法公式是解题关键．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，连接DE交AC于点F．
13．
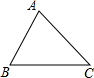如图，△ABC是锐角三角形，sinC=$\frac{4}{5}$，则sinA的取值范围是（ ）
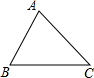如图，△ABC是锐角三角形，sinC=$\frac{4}{5}$，则sinA的取值范围是（ ）| A． | 0$＜sinA＜\frac{3}{5}$ | B． | $\frac{4}{5}＜sinA＜1$ | C． | $\frac{3}{5}＜sinA＜\frac{4}{5}$ | D． | $\frac{3}{5}＜sinA＜1$ |
3．
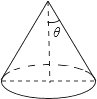已知圆锥的底面半径为3cm，侧面积为15πcm2，设圆锥的母线与高的夹角为θ（如图所示），则tanθ的值为（ ）
已知圆锥的底面半径为3cm，侧面积为15πcm2，设圆锥的母线与高的夹角为θ（如图所示），则tanθ的值为（ ）| A． | $\frac{3}{5}$ | B． | $\frac{3}{4}$ | C． | $\frac{4}{3}$ | D． | $\frac{4}{5}$ |
7．已知x+y=6，xy=4，则x2y+xy2的值为（ ）
| A． | 12 | B． | -12 | C． | -24 | D． | 24 |
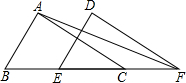如图，已知△ABC的面积为16，BC=8，∠ACB=42°，现将△ABC沿直线BC向右平移a个单位到△DEF