题目内容

14．若mn≠0，已知mx=nx，则下列结论成立的是（　　）
A．x=0B．m，n一定相等C．x=$\frac{n}{m}$D．x的解不确定

分析 根据等式的基本性质进行选择即可．

解答 解：∵mn≠0，mx=nx，x≠0，
∴m=n，
当x=0时，m≠n，
故选D．

点评 本题考查了等式的性质，掌握等式的性质解题的关键．

练习册系列答案
相关题目
7．斐波那契（约1170-1250，意大利数学家）数列是按某种规律排列的一列数，他发现该数列中的每个正整数都可以用无理数的形式表示，如第n（n为正整数）个数an可表示为$\frac{1}{\sqrt{5}}$[（$\frac{1+\sqrt{5}}{2}$）n-（$\frac{1-\sqrt{5}}{2}$）n]．
（1）计算第一个数a1；
（2）计算第二个数a2；
（3）证明连续三个数之间an-1，an，an+1存在以下关系：an+1-an=an-1（n≥2）；
（4）写出斐波那契数列中的前8个数．
8．计算：
（1）（-1）2017-23+（cos68°+$\frac{5}{π}$）0+|3$\sqrt{3}$-8sin60°|；
（2）$\sqrt{2}$cos45°-tan30°•sin60°．
2．某次篮球联赛共有十支队伍参赛，部分积分表如下：
队名比赛场次胜场负场积分
A1612428
B1610626
C168824
D1601616
其中一队的胜场总积分能否等于负场总积分？请说明理由．
9．计算：6ab（2a+3b）=12a2b+18ab2．
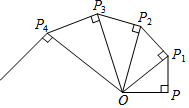19．如图OP=1，过P作PP1⊥OP，得$O{P_1}=\sqrt{2}$；再过P1作PP2⊥OP1且PP2=1，得$O{P_2}=\sqrt{3}$；又过P2作P2P3⊥OP2且P2P3=1，得：OP3=2；…依此法继续作下去，得OP2014=$\sqrt{2015}$．
6．若k为正整数，则2•（-2）2k+（-2）2k+1等于（　　）
A．0B．22k+1C．-22k+1D．22k+2
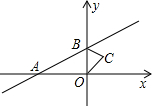3．如图，直线y=x+1与x轴交于点A，与y轴交于点B，△BOC与△B′O′C′是以点A为位似中心的位似图形，且相似比为1：3，则点B的对应点B′的坐标为（-4，-3）或（2，3）．
4．2617与8213的大小关系是（　　）
A．2617＞8213B．2617=8213C．2617＜8213D．不能判定

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网