题目内容
7.斐波那契(约1170-1250,意大利数学家)数列是按某种规律排列的一列数,他发现该数列中的每个正整数都可以用无理数的形式表示,如第n(n为正整数)个数an可表示为$\frac{1}{\sqrt{5}}$[($\frac{1+\sqrt{5}}{2}$)n-($\frac{1-\sqrt{5}}{2}$)n].(1)计算第一个数a1;
(2)计算第二个数a2;
(3)证明连续三个数之间an-1,an,an+1存在以下关系:an+1-an=an-1(n≥2);
(4)写出斐波那契数列中的前8个数.
分析 (1)(2)代入计算即可求解;
(3)根据乘法分配律即可证明:an+1-an=an-1(n≥2);
(4)根据(3)的关系可求斐波那契数列中的前8个数.
解答 解:(1)a1=$\frac{1}{\sqrt{5}}$[($\frac{1+\sqrt{5}}{2}$)-($\frac{1-\sqrt{5}}{2}$)]=$\frac{1}{\sqrt{5}}$×$\sqrt{5}$=1;
(2)a2=$\frac{1}{\sqrt{5}}$[($\frac{1+\sqrt{5}}{2}$)2-($\frac{1-\sqrt{5}}{2}$)2]=$\frac{1}{\sqrt{5}}$×$\sqrt{5}$=1;
(3)证明:an+1-an=$\frac{1}{\sqrt{5}}$[($\frac{1+\sqrt{5}}{2}$)n+1-($\frac{1-\sqrt{5}}{2}$)n+1]-$\frac{1}{\sqrt{5}}$[($\frac{1+\sqrt{5}}{2}$)n-($\frac{1-\sqrt{5}}{2}$)n]
=$\frac{1}{\sqrt{5}}$[($\frac{1+\sqrt{5}}{2}$)n+1-($\frac{1+\sqrt{5}}{2}$)n]-$\frac{1}{\sqrt{5}}$[($\frac{1-\sqrt{5}}{2}$)n+1-($\frac{1-\sqrt{5}}{2}$)n]
=$\frac{1}{\sqrt{5}}$[($\frac{1+\sqrt{5}}{2}$)n($\frac{1+\sqrt{5}}{2}$-1)]-$\frac{1}{\sqrt{5}}$[($\frac{1-\sqrt{5}}{2}$)n($\frac{1-\sqrt{5}}{2}$-1)]
=$\frac{1}{\sqrt{5}}$[($\frac{1+\sqrt{5}}{2}$)n($\frac{\sqrt{5}-1}{2}$)]-$\frac{1}{\sqrt{5}}$[($\frac{1-\sqrt{5}}{2}$)n(-$\frac{1+\sqrt{5}}{2}$)]
=$\frac{1}{\sqrt{5}}$[($\frac{1+\sqrt{5}}{2}$)n-1-($\frac{1-\sqrt{5}}{2}$)n-1];
(4)斐波那契数列中的前8个数是1,1,2,3,5,8,13,21.
点评 此题考查了二次根式的应用,关键是熟悉斐波那契数列的规律.

| A. | $\frac{1}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{6}$ | D. | $\frac{2}{5}$ |
| A. | x=0 | B. | m,n一定相等 | C. | x=$\frac{n}{m}$ | D. | x的解不确定 |
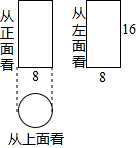 如图是一个几何体从三个方向看所得到的形状图,则该几何体的表面积为160π(结果保留π)
如图是一个几何体从三个方向看所得到的形状图,则该几何体的表面积为160π(结果保留π) 如图△PAB中,PA=PB,PB为⊙O的切线,B为切点,连接OP交AB于点C,延长BO与⊙O交于点D、与PA的延长线交于点E
如图△PAB中,PA=PB,PB为⊙O的切线,B为切点,连接OP交AB于点C,延长BO与⊙O交于点D、与PA的延长线交于点E 如图,在矩形ABCD中,点O在对角线AB上,以OA的长为半径的圆O与AD交于点E,且∠ACB=∠DCE,求证:CE是⊙O的切线.
如图,在矩形ABCD中,点O在对角线AB上,以OA的长为半径的圆O与AD交于点E,且∠ACB=∠DCE,求证:CE是⊙O的切线.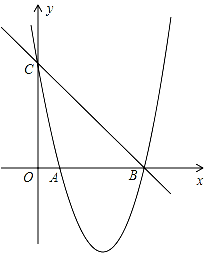 如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).
如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).